Треугольник. Вычисление периметра
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Треугольники играют важную роль в математике и реальном мире благодаря своим свойствам и разнообразным видам.
Виды треугольников:
- Обычный треугольник – это треугольник, у которого все его стороны и углы между ними различны.
- Прямоугольный треугольник – это треугольник, у которого один из его углов является прямым (равным 90 градусов). Гипотенуза – это сторона противоположная прямому углу, а катеты – это стороны, образующие прямой угол.
- Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой, что влечет за собой равенство двух соответствующих углов.
- Равносторонний треугольник – это треугольник, у которого все стороны равны между собой, и все его углы равны 60 градусам.
Свойства треугольников:
- Сумма углов в любом треугольнике всегда равна 180 градусам.
- В прямоугольном треугольнике, гипотенуза (самая длинная сторона) всегда больше любого из катетов.
- В равнобедренном треугольнике, биссектриса угла при основании делит его на два равных угла и равные стороны.
- В равностороннем треугольнике, биссектриса, медиана и высота совпадают.
Вычисление периметра треугольника:
Периметр треугольника – это сумма длин его сторон. Для различных типов треугольников, есть различные формулы для вычисления периметра:
Периметр треугольника через стороны (формула)
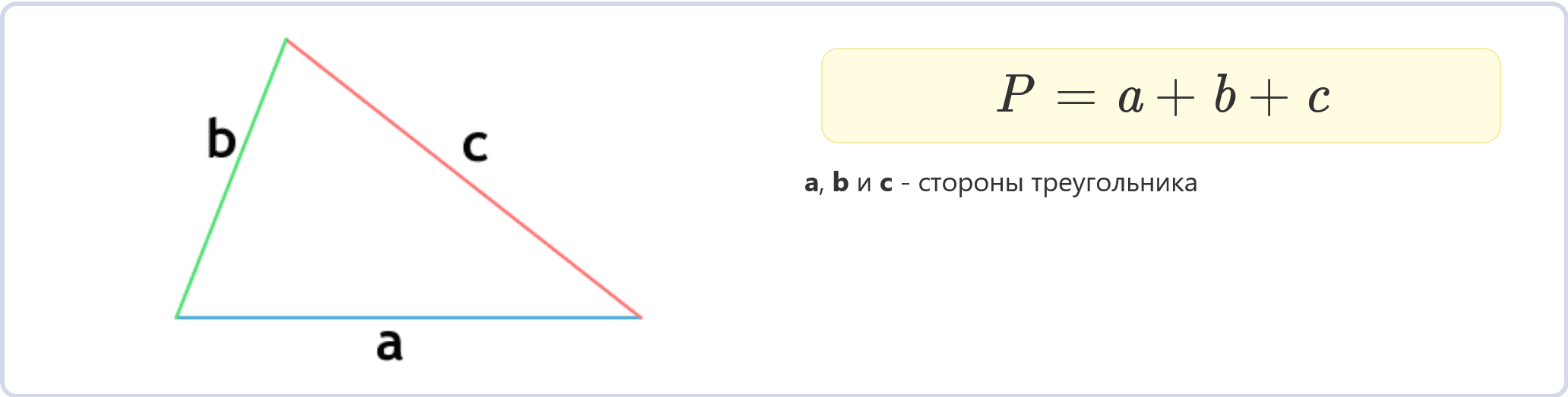
P = a + b + c
где a, b и c – длины сторон треугольника.
Периметр треугольника по средним линиям (медианам) (формула)
Средняя линия треугольника — отрезок, который соединяет середины двух сторон.
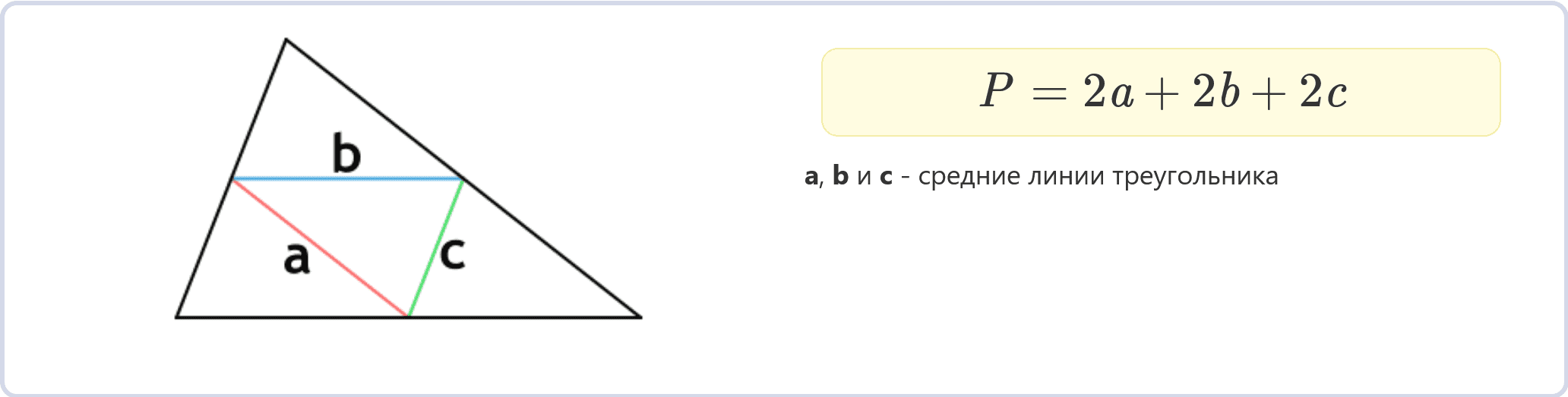
P = 2a + 2b + 2c
a, b и c – средние линии треугольника
Периметр треугольника по двум сторонам и углу между ними (формула)
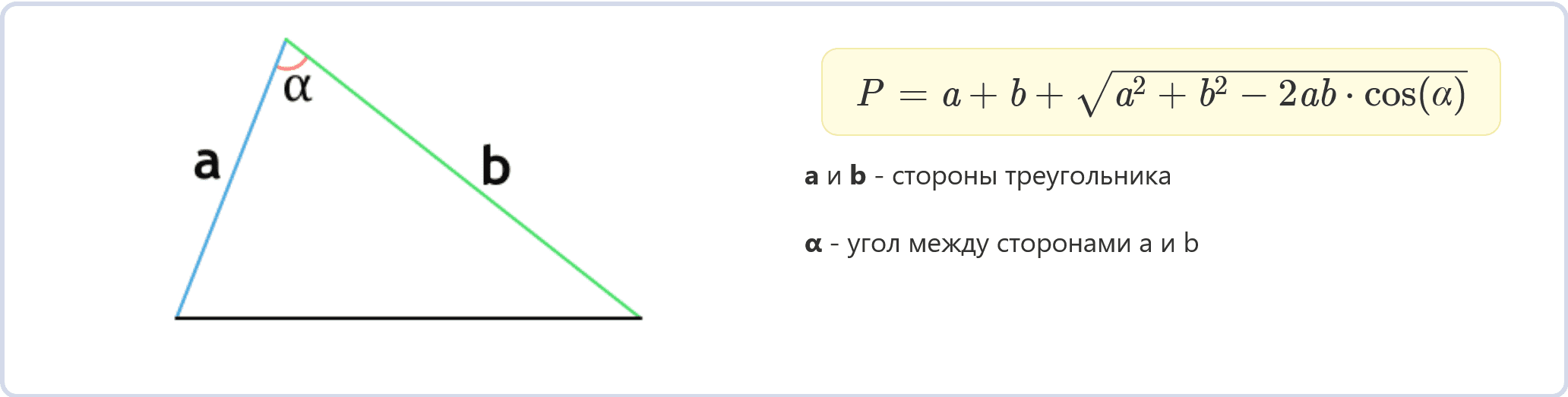
P = a + b + √(a² + b² − 2ab ⋅ cos(α))
a и b – стороны треугольника
α – угол между сторонами a и b
Периметр прямоугольного треугольника по катету и гипотенузе (формула)
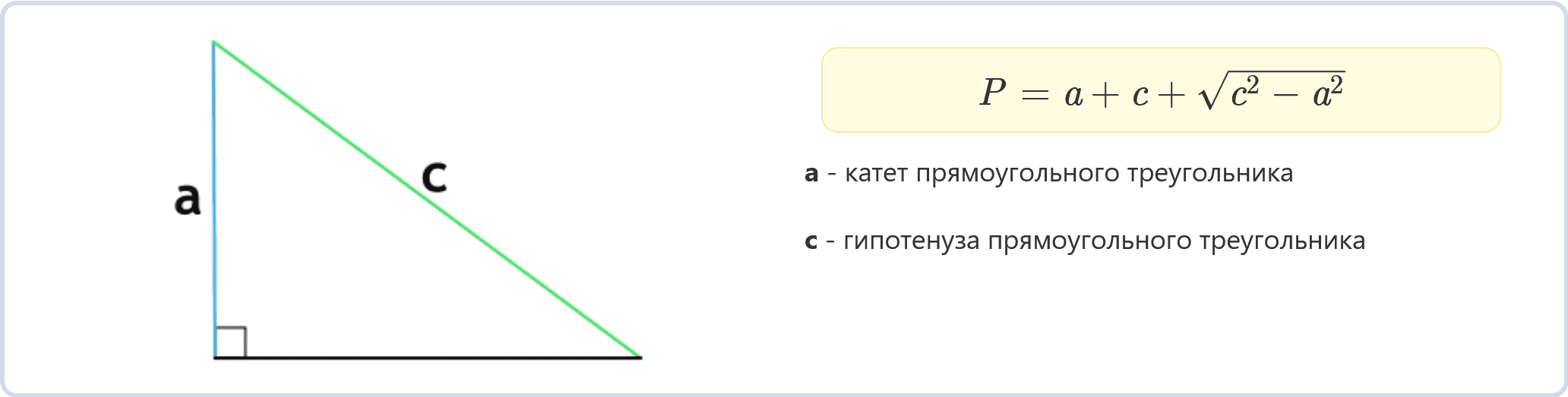
P = a + c + √(c² − a²)
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Периметр прямоугольного треугольника по катетам (формула)
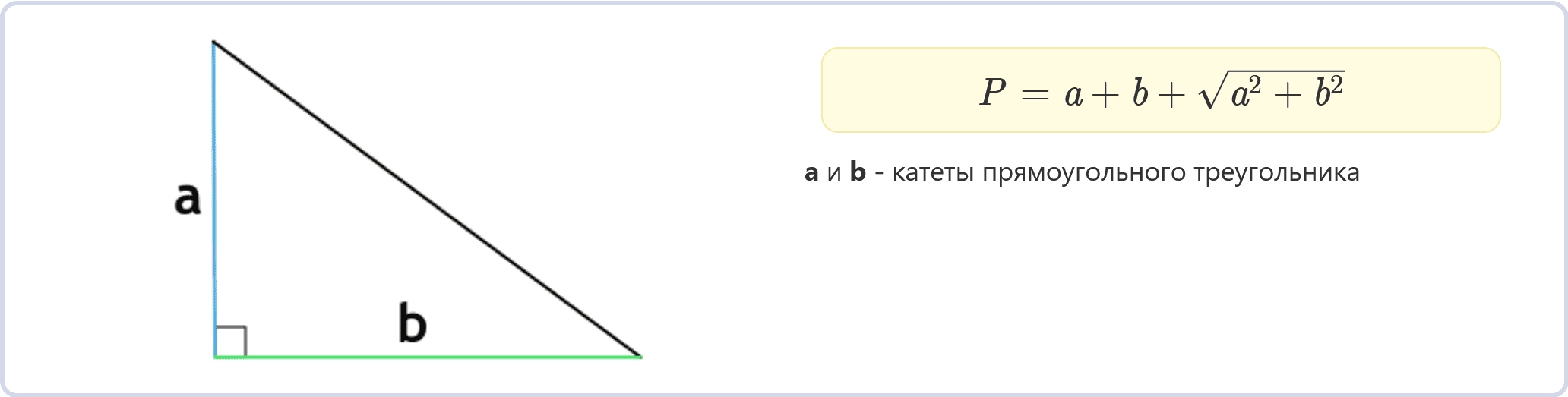
P = a + b + √(a² + b²)
a и b – катеты прямоугольного треугольника
Периметр прямоугольного треугольника по гипотенузе и прилежащему углу (формула)

P = csin(α) + ccos(α) + c
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе угол
Периметр прямоугольного треугольника по катету и прилежащему углу (формула)
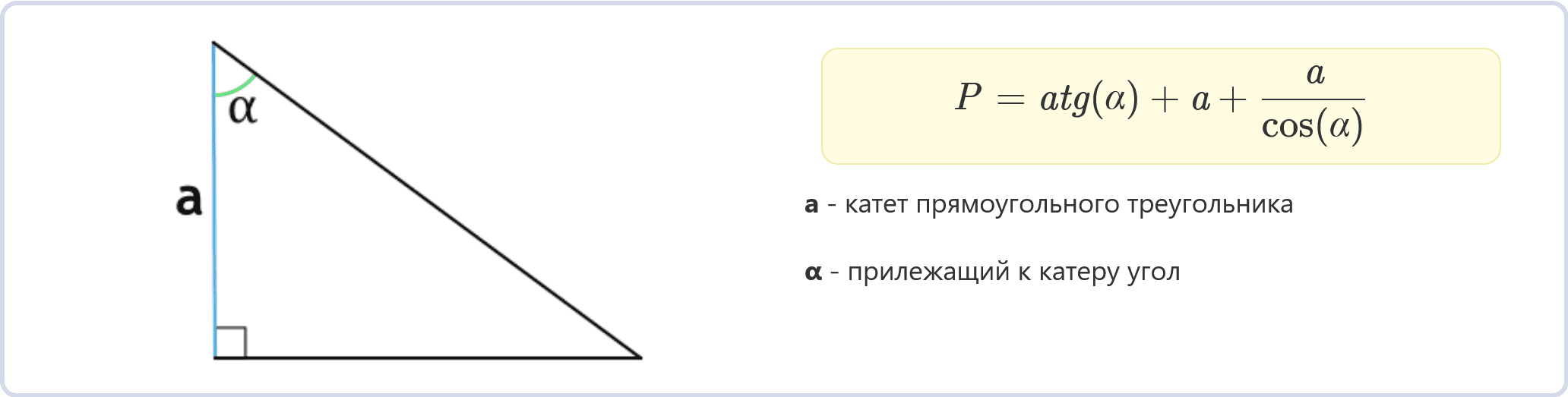
P = atg(α) + a + a/cos(α)
a – катет прямоугольного треугольника
α – прилежащий к катеру угол
Периметр прямоугольного треугольника по катету и противолежащему углу (формула)
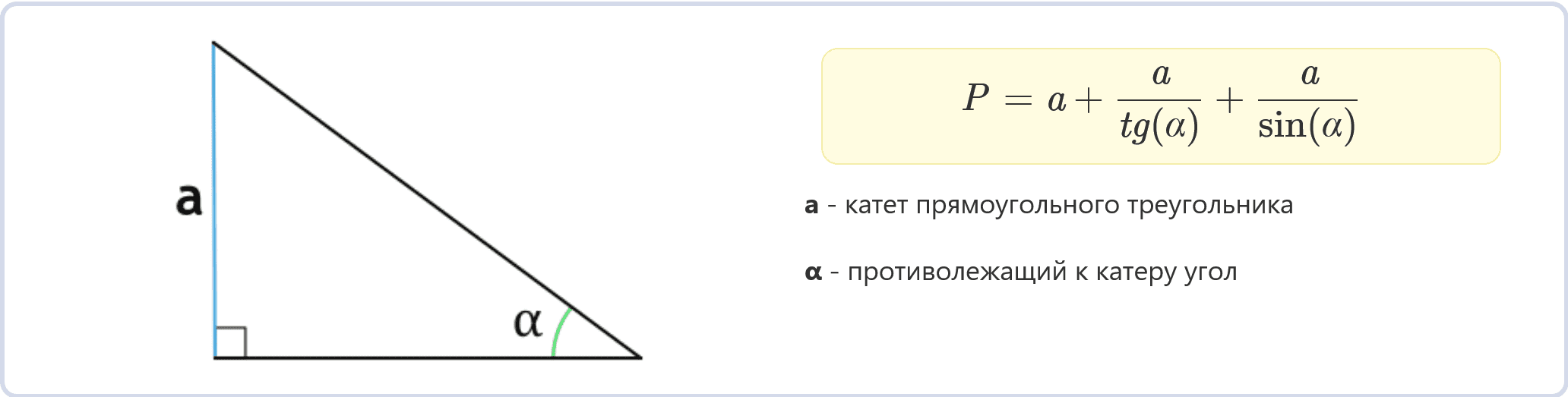
P = a + a/tg(α) + a/sin(α)
a – катет прямоугольного треугольника
α – противолежащий к катеру угол
Периметр равнобедренного треугольника по боковой стороне и высоте (формула)
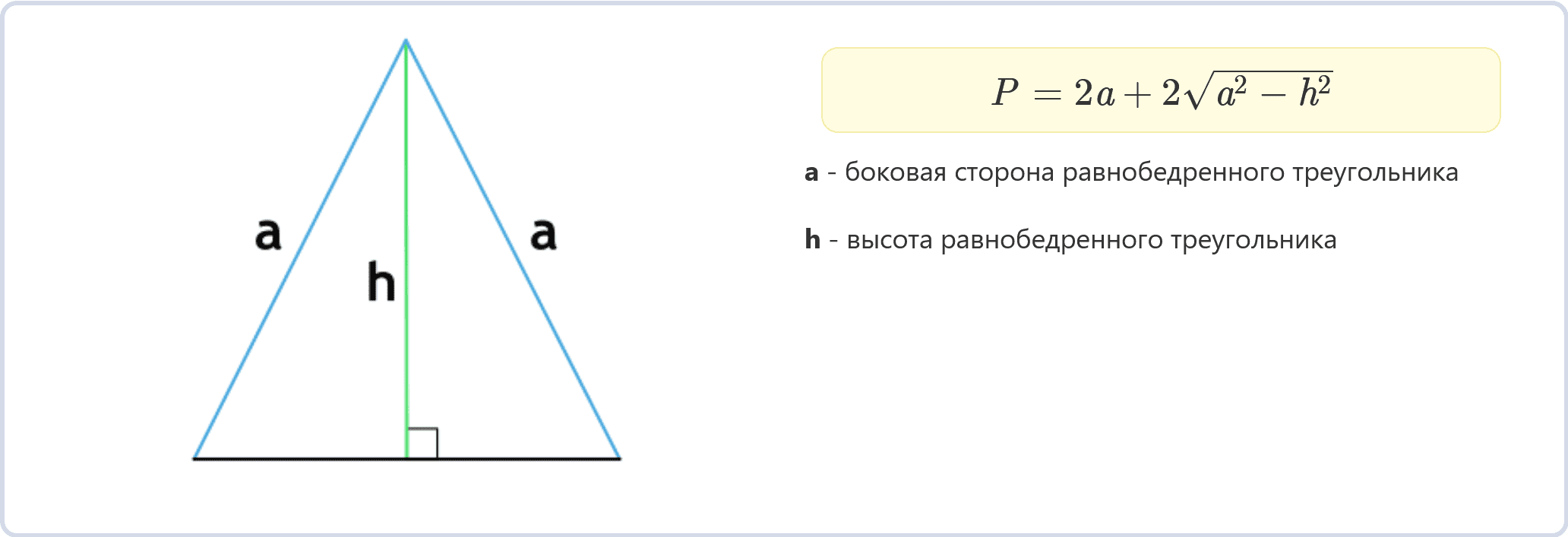
P = 2a + 2√(a² − h²)
a – боковая сторона равнобедренного треугольника
h – высота равнобедренного треугольника
Периметр равнобедренного треугольника по основанию и высоте (формула)
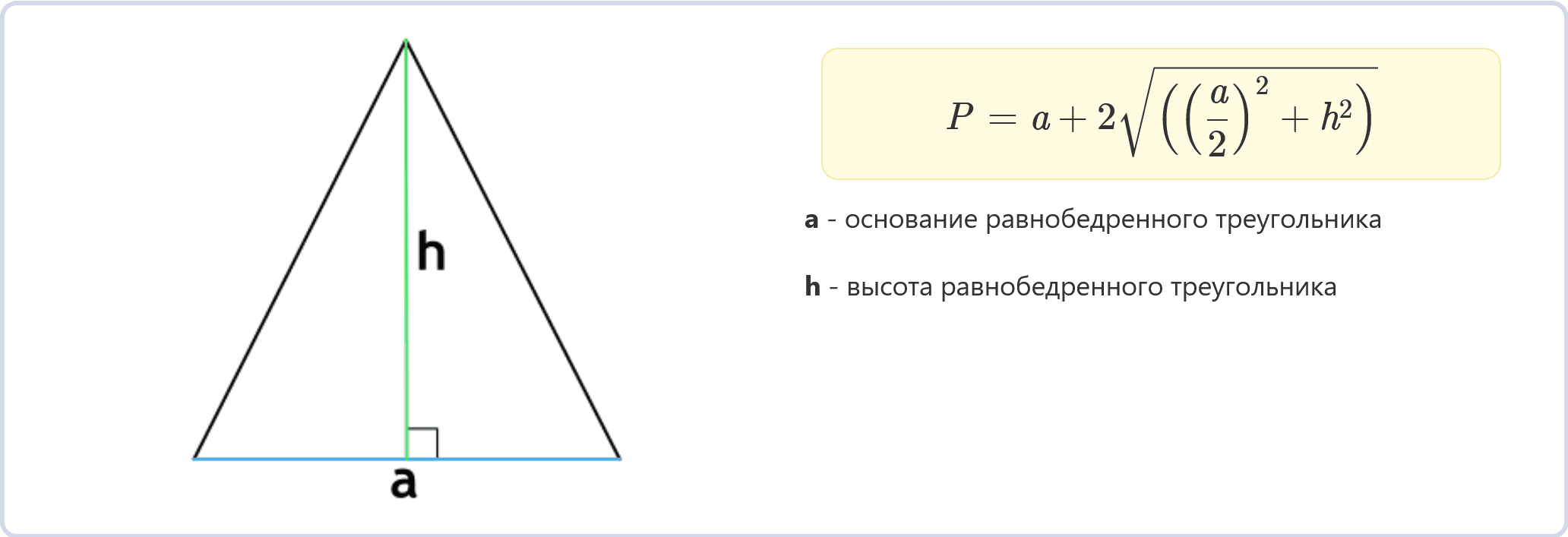
P = a + 2√((a/2)² + h²)
a – основание равнобедренного треугольника
h – высота равнобедренного треугольника
Периметр равнобедренного треугольника по боковой стороне и основанию (формула)
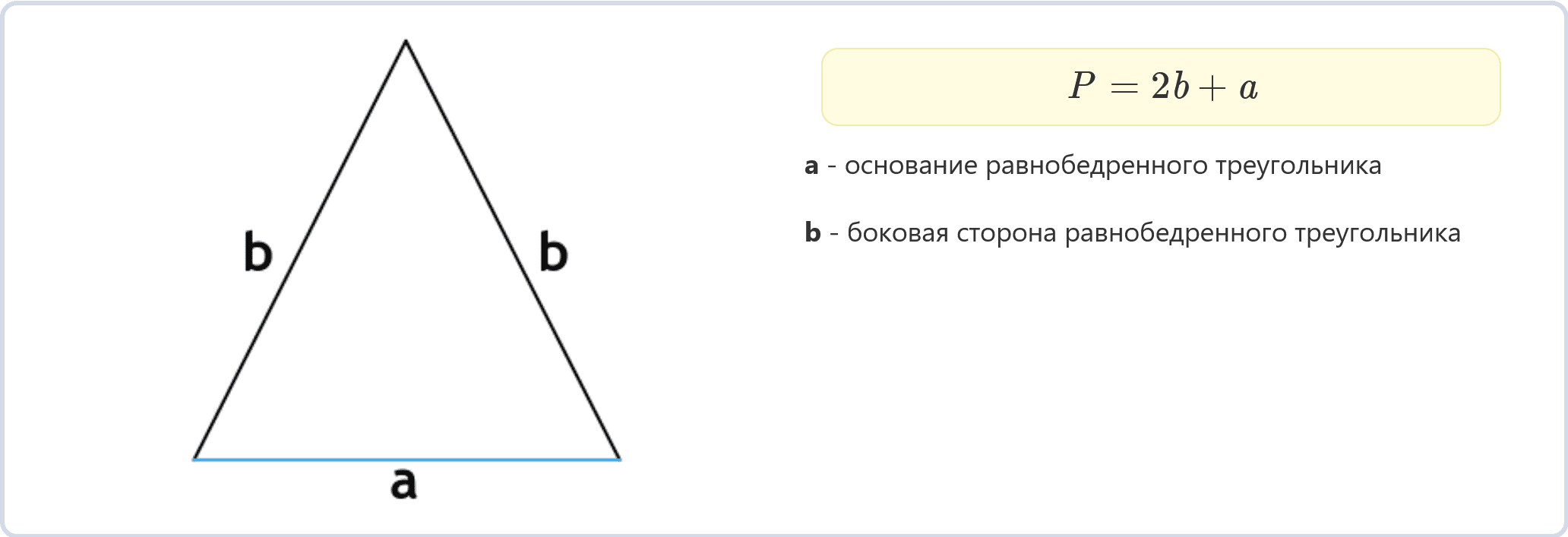
P = 2b + a
a – основание равнобедренного треугольника
b – боковая сторона равнобедренного треугольника
Периметр равностороннего треугольника по высоте (формула)
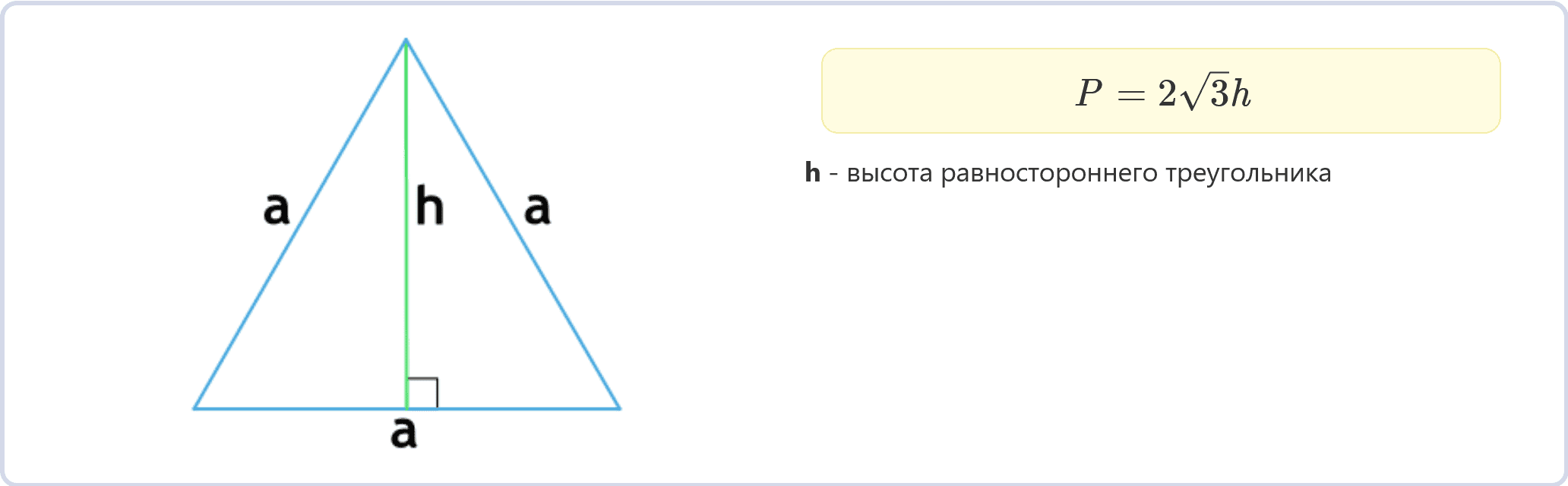
P = 2√(3h)
h – высота равностороннего треугольника
Периметр равностороннего треугольника через площадь вписанной окружности (формула)
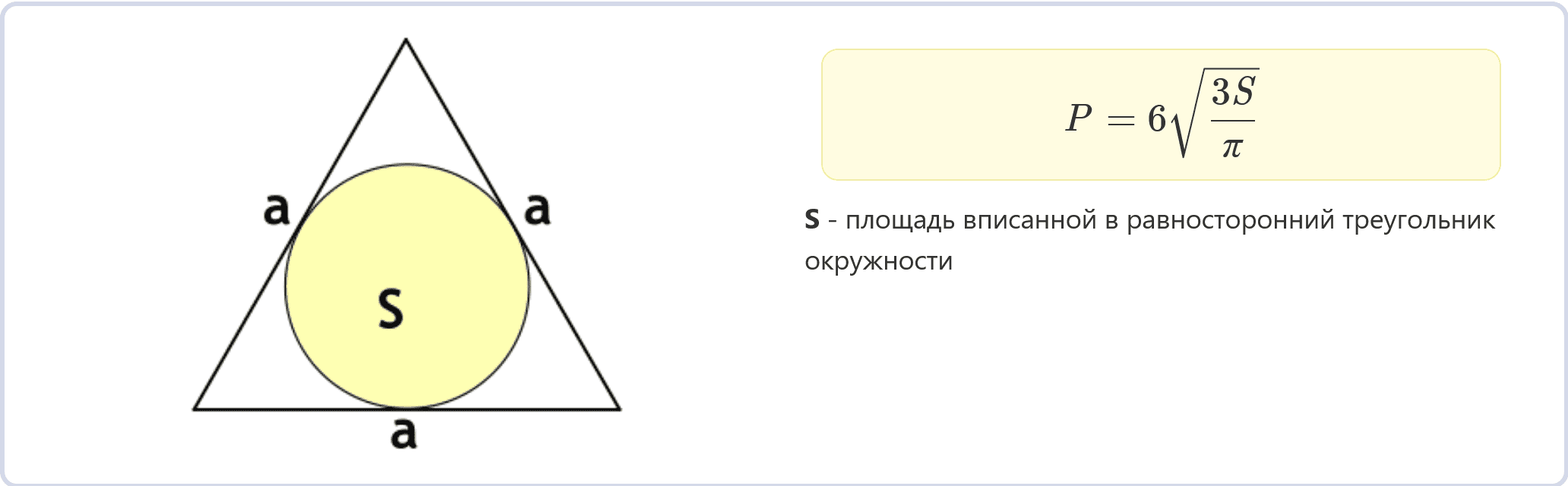
P = 6√(3S/π)
S – площадь вписанной в равносторонний треугольник окружности
Треугольники обладают богатым набором свойств и формул, которые находят применение как в математике, так и в практических задачах. Их изучение и понимание помогают не только в геометрии, но и в других областях науки и инженерии
Заключение
Треугольник, являясь одной из фундаментальных геометрических фигур, обладает богатым набором свойств и характеристик, которые оказывают влияние как в математике, так и в практических областях. Изучение его особенностей позволяет нам лучше понимать структуру пространства и взаимосвязи между его сторонами и углами.
Разнообразие типов треугольников – от обычных до специфических, таких как прямоугольные, равносторонние и равнобедренные, – предоставляет нам широкий спектр применений в различных сферах. От архитектуры до науки о материалах, от инженерии до астрономии, понимание свойств треугольников играет важную роль.
Вычисление периметра – один из фундаментальных аспектов изучения треугольников. Формулы для вычисления периметра в разных типах треугольников облегчают решение задач, связанных с длинами его сторон. От простых обычных треугольников до более сложных прямоугольных, равнобедренных и равносторонних – каждая формула имеет свою уникальность и применимость.
Изучение треугольников продолжает оставаться актуальным и интересным для ученых, студентов и практиков. Ведь даже в современном мире, где технологии играют огромную роль, базовые геометрические понятия остаются неотъемлемой частью понимания окружающего нас пространства.
В заключении можно сказать, что треугольник – это не только математическая фигура, но и символ знаний, исследований и практических приложений. Его уникальные свойства и разнообразие типов делают его неотъемлемой частью образования и научного прогресса.
Полезен ли материал?
5 / 10

