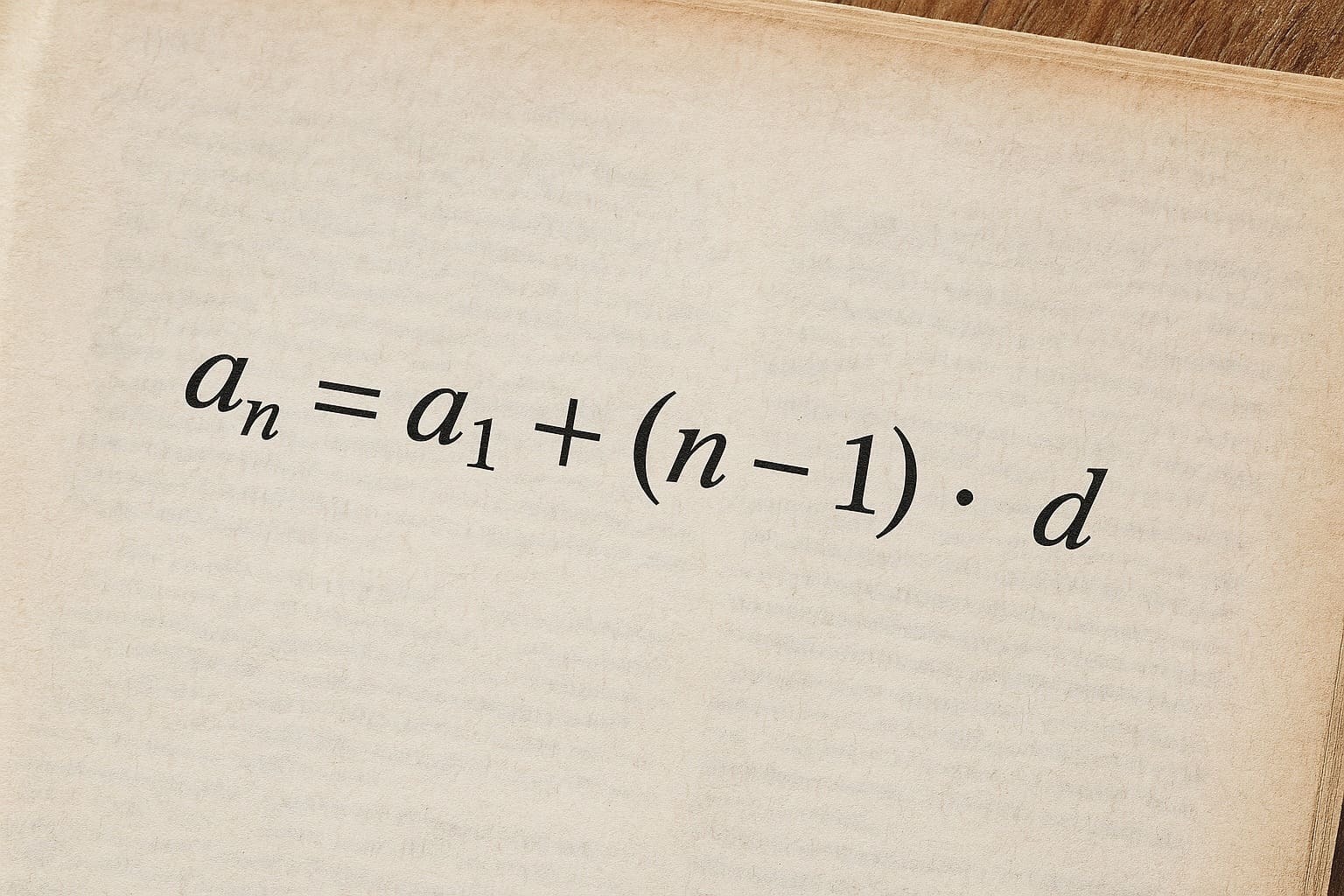
Как найти любой член арифметической прогрессии: полное руководство
Арифметическая прогрессия — это последовательность чисел, где каждый следующий член отличается от предыдущего на постоянную величину, называемую разностью прогрессии (d). Умение находить конкретный член такой последовательности — фундаментальный математический навык с широким практическим применением.
Арифметические прогрессии встречаются повсеместно: в финансовых расчетах (регулярные платежи), физике (равномерное движение), компьютерных алгоритмах и даже в повседневном планировании.
Основная формула для нахождения n-го члена
Где:
- an — n-й член прогрессии, который мы хотим найти
- a1 — первый член прогрессии
- n — порядковый номер искомого члена
- d — разность прогрессии (d = an+1 – an)
Эта формула позволяет найти любой член прогрессии, зная первый член и разность.
Подробные примеры расчетов
Пример 1: Возрастающая прогрессия
Условие: Найти 5-й член прогрессии с a1 = 3 и d = 2.
Решение по шагам:
Ответ: Пятый член прогрессии равен 11.
Пример 2: Убывающая прогрессия
Условие: Найти 7-й член прогрессии с a1 = 10 и d = -3.
Решение по шагам:
Ответ: Седьмой член прогрессии равен -8.
Обратите внимание, что при отрицательной разности прогрессия убывает.
Онлайн-калькулятор членов арифметической прогрессии
Современные онлайн-калькуляторы значительно упрощают нахождение членов прогрессии:
- Вы вводите первый член прогрессии (a1)
- Указываете разность (d)
- Задаете номер искомого члена (n)
- Получаете мгновенный точный результат
Преимущества использования калькулятора:
- Мгновенные расчеты без ручных вычислений
- Исключение арифметических ошибок
- Возможность работы с дробными и большими числами
- Часто — пошаговое отображение решения
- Доступность с любого устройства
Практическое применение в реальной жизни
1. Финансы и банковское дело:
- Расчет суммы регулярных платежей по кредиту
- Планирование накоплений с фиксированным ежемесячным пополнением
- Прогнозирование роста доходов или расходов
2. Физика и инженерия:
- Определение положения объекта при равномерном движении
- Расчет температурных изменений с постоянной скоростью
- Анализ линейных изменений различных физических величин
3. Компьютерные технологии:
- Генерация последовательностей чисел в программировании
- Создание равномерных шкал и графиков
- Оптимизация алгоритмов с линейной сложностью
4. Повседневное планирование:
- Составление плана тренировок с постепенным увеличением нагрузки
- Планирование учебного графика с возрастающей сложностью
- Организация любых процессов с линейным развитием
Ответы на частые вопросы
Разность вычисляется как разница между любыми двумя последовательными членами: d = an+1 – an. Например, если известны a2 = 5 и a3 = 8, то d = 8 – 5 = 3.
Да, формулу можно преобразовать: a1 = an – (n – 1) × d. Например, если a5 = 20 и d = 3, то a1 = 20 – (5-1)×3 = 20 – 12 = 8.
Формула работает одинаково для любых чисел — целых, дробных, положительных и отрицательных. Просто выполняйте арифметические действия с дробями по обычным правилам.
Да, из основной формулы можно выразить n: n = (an – a1)/d + 1. Например, если a1 = 2, d = 3 и an = 20, то n = (20-2)/3 + 1 ≈ 7 (округляем до целого).
Формула позволяет сразу найти любой член, не вычисляя все предыдущие, что особенно важно для больших значений n (например, найти 1000-й член).
Заключение
Формула an = a1 + (n – 1) × d — мощный инструмент для работы с арифметическими прогрессиями. Она находит применение в самых разных областях — от финансового планирования до физических расчетов.
Освоив эту формулу, вы сможете:
- Быстро находить любой член прогрессии
- Решать сложные задачи без последовательных вычислений
- Применять эти знания в практических ситуациях
- Лучше понимать линейные процессы в различных областях
Для сложных расчетов или проверки своих решений используйте специализированные калькуляторы членов арифметической прогрессии.
Полезен ли материал?
14 / 10

