Длина дуги окружности
Длина дуги окружности – это расстояние по кривой линии, измеряемое вдоль дуги окружности между двумя её конечными точками. Рассмотрим более подробно, что такое длина дуги окружности, как её вычислять через различные параметры, и какие особенности этой величины.
Основные понятия
Прежде чем перейти к длине дуги окружности, давайте разберёмся с основными понятиями, связанными с окружностью:
- Окружность: Это геометрическая фигура, состоящая из всех точек в плоскости, которые находятся на одинаковом расстоянии от одной точки, называемой центром окружности.
- Радиус (R): Расстояние от центра окружности до любой точки на её окружности.
- Диаметр (D): Двукратное расстояние от центра окружности до точки на противоположной стороне окружности. Диаметр равен удвоенному радиусу, т.е. D = 2R.
- Центральный угол (α): Угол между двумя радиусами, проведёнными из центра окружности к её конечным точкам.
Формулы для вычисления длины дуги
Длина дуги (L) окружности зависит от радиуса и центрального угла между конечными точками дуги. Существует несколько способов вычисления длины дуги (L) в зависимости от данных параметров:
Через радиус и угол в градусах
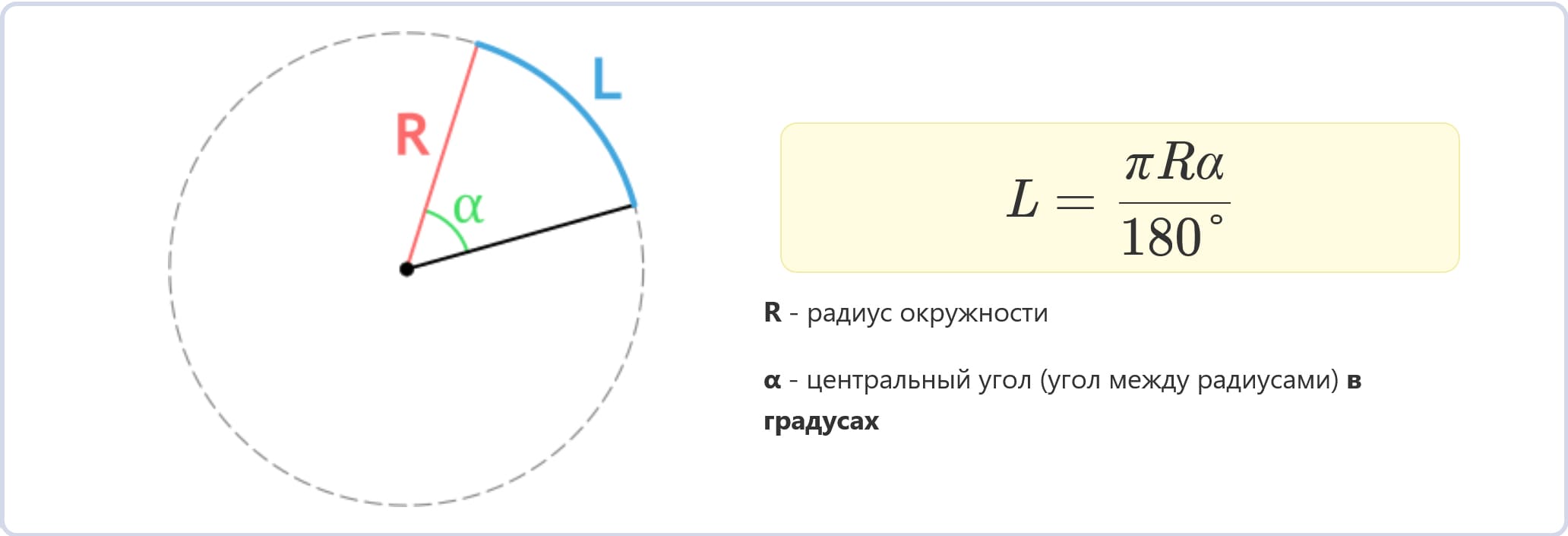
L = (πRα) / 180°
Где R – радиус, α – центральный угол в градусах.
Через радиус и угол в радианах
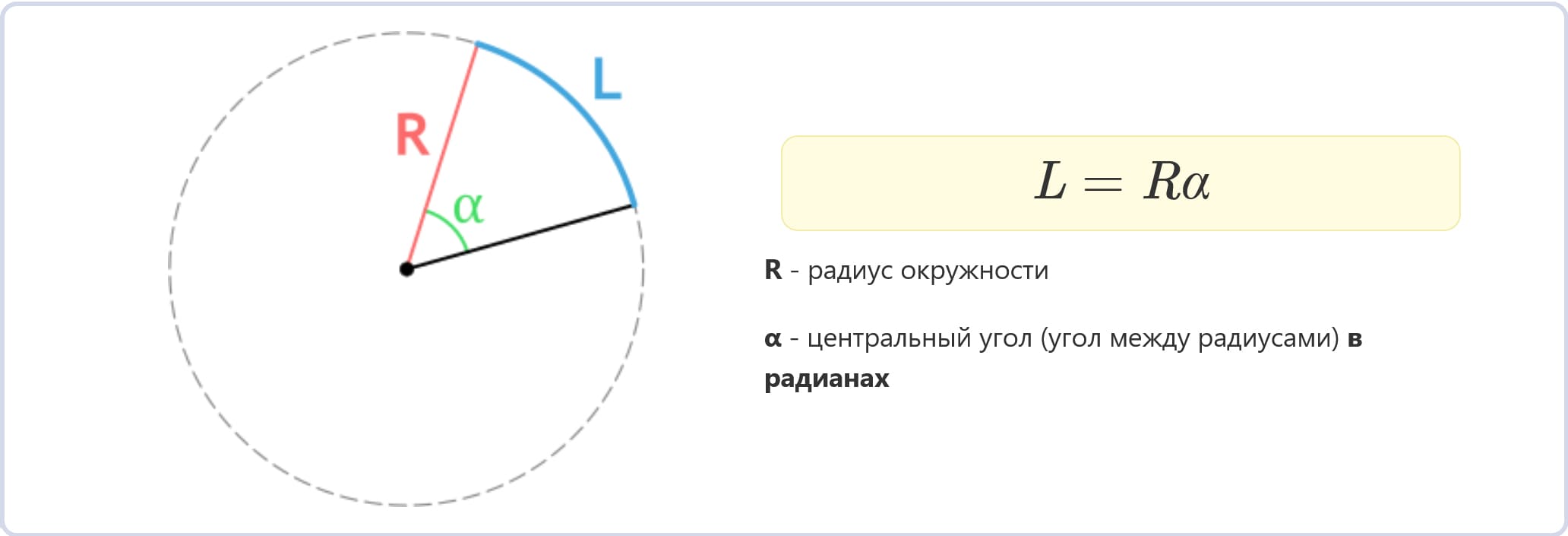
L = Rα
Где R – радиус, α – центральный угол в радианах.
По формуле Гюйгенса
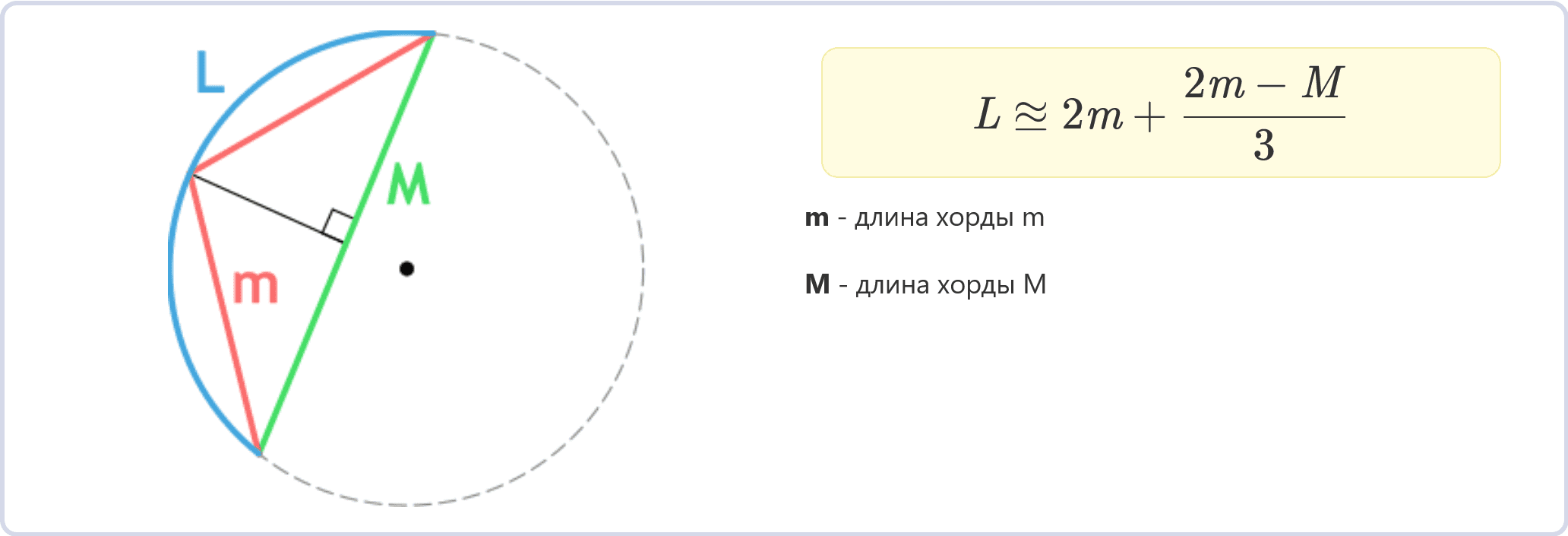
L 2m + ((2m – M) / 3)
Где m и M – длины хорды, связанные с центральным углом α, и 2m > M.
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «≊». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Применение и особенности
Вычисление длины дуги окружности находит своё применение в геометрии, физике, инженерии и других научных областях. Особенно она полезна, когда требуется вычислить путь, который объект совершает вдоль окружности при вращении вокруг центра.
Важно отметить, что длина дуги зависит от центрального угла. Чем больше угол, тем длиннее дуга. Кроме того, если угол стремится к 360° (или 2π радиан), длина дуги становится равной окружности, т.е. L = 2πR или D.
Заключение
Длина дуги окружности представляет собой интересную и важную математическую величину, которая находит применение в различных областях. Её вычисление может быть выполнено через радиус и центральный угол, а также с использованием формулы Гюйгенса. Понимание этой концепции позволяет более глубоко вникнуть в геометрию окружностей и их свойства.
Полезен ли материал?
47 / 14

