Параллелограмм и его периметр
Параллелограмм – это геометрическая фигура, которая имеет множество интересных свойств и применений. Одним из ключевых аспектов, определяющих его форму и размер, является периметр. Периметр – это сумма длин всех сторон фигуры. В этой статье мы рассмотрим формулы для расчета периметра параллелограмма через его стороны и диагонали.
Формула периметра через две стороны
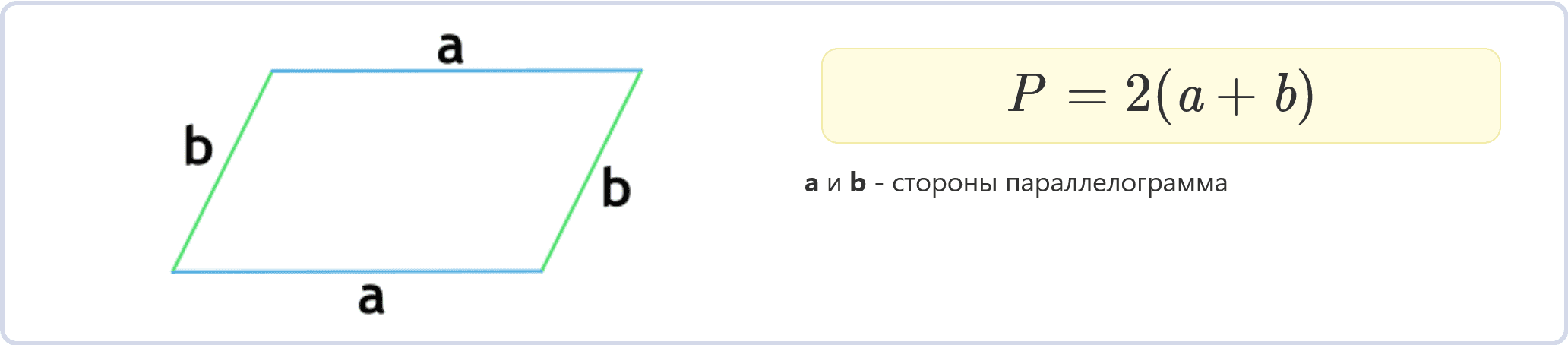
Периметр параллелограмма можно выразить с использованием длин двух его сторон. Пусть a и b – длины двух сторон параллелограмма. Тогда формула для вычисления периметра P будет следующей:
P = 2 (a + b)
Эта формула основывается на том, что параллелограмм имеет две пары параллельных сторон. Следовательно, периметр можно выразить как сумму длин двух параллельных сторон, умноженную на 2.
Формула периметра через диагонали и сторону
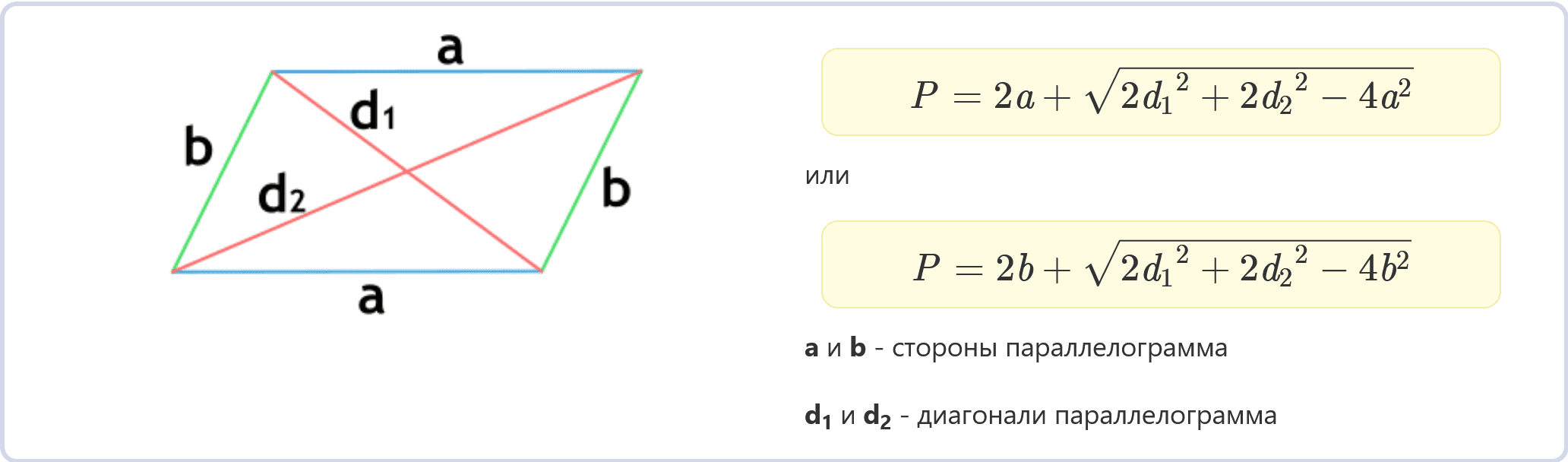
Существует также формула для вычисления периметра параллелограмма с использованием длин его диагоналей и одной из сторон. Обозначим a или b как длины сторон параллелограмма, а d₁ и d₂ – длины его диагоналей. Тогда формула для вычисления периметра P будет следующей:
P = 2a+√(2d12 + 2d22 – 4a2)
или
P = 2b+√(2d12 + 2d22 – 4b2)
Эта формула может показаться сложной на первый взгляд, но она основывается на том, что диагонали параллелограмма делят его на четыре треугольника. При использовании теоремы Пифагора для этих треугольников и сложении результатов мы получаем формулу для периметра.
Применение формул
Знание этих формул позволяет легко вычислять периметр параллелограмма, используя различные известные параметры. Например, если известны длины сторон, то можно воспользоваться первой формулой. Если известны длины диагоналей и одной стороны, то подходит вторая формула.
Заключение
Периметр параллелограмма является важным атрибутом его формы и размера. Знание формул для вычисления периметра через стороны и диагонали позволяет эффективно решать задачи, связанные с этой геометрической фигурой. Независимо от того, используете ли вы простую формулу через стороны или более сложную через диагонали, вы сможете точно определить периметр параллелограмма и использовать этот результат в дальнейших вычислениях и решениях задач.
Полезен ли материал?
4 / 1

