Прямоугольник. Периметр

Прямоугольник – это одна из наиболее распространенных геометрических фигур, которая играет важную роль в различных областях, начиная от геометрии и заканчивая архитектурой. У прямоугольника есть свои характерные свойства, и его периметр – это один из основных параметров, который определяет длину его контура.

Основные свойства прямоугольника

1. Углы прямоугольника: Прямоугольник имеет четыре угла, каждый из которых равен 90 градусов. Эти углы являются прямыми.
2. Противоположные стороны равны: Противоположные стороны прямоугольника равны между собой. Это означает, что длины двух пар противоположных сторон “a” и “b” одинаковы.
3. Диагонали прямоугольника: Диагонали прямоугольника имеют равные длины и делят его на два равных прямоугольных треугольника. Обозначим длины диагоналей как “d₁” и “d₂“.

Периметр прямоугольника

Периметр прямоугольника – это сумма длин всех его сторон. Для прямоугольника с сторонами “a” и “b”, периметр можно выразить двумя разными способами:

Через стороны

Периметр прямоугольника по формуле через стороны выглядит следующим образом:

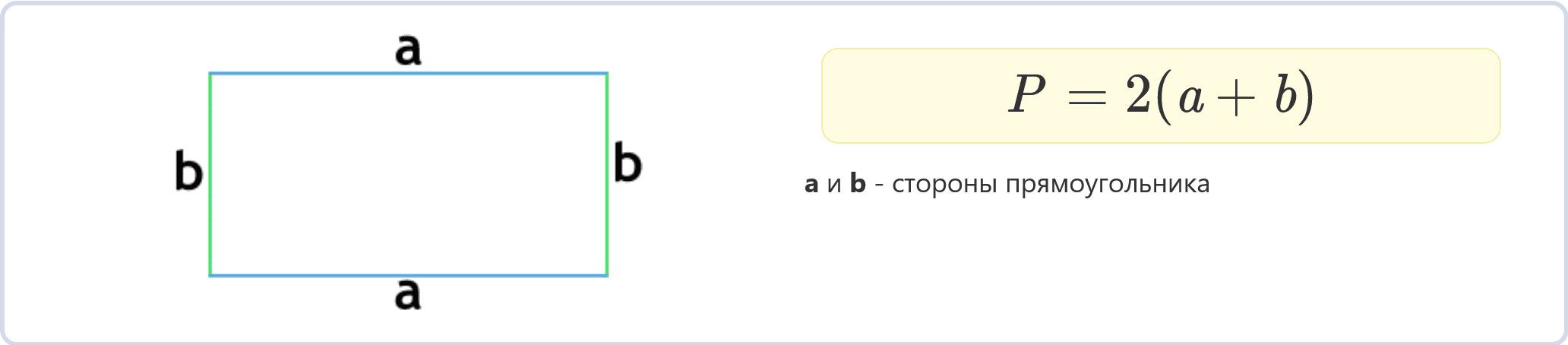
P = 2∙(a + b)

a и b – стороны прямоугольника

Через диагональ и сторону

Также можно выразить периметр прямоугольника через диагональ и одну из сторон:

P = 2∙(a + √(d² – a²))

где a – сторона прямоугольника, d – диагональ.

Практическое применение

Прямоугольники используются в различных областях: от строительства и дизайна до инженерии и математики. Знание свойств прямоугольника и способов расчета его периметра позволяет эффективно работать с этой фигурой, а также применять ее в практических задачах.

Заключение

Прямоугольник – это геометрическая фигура с уникальными свойствами, обладающая прямыми углами и равными противоположными сторонами. Расчет периметра прямоугольника важен для определения его размеров и применения в различных областях, где форма прямоугольника играет ключевую роль.

Полезен ли материал?

ДаНет

6 / 1

#Калькуляторы #Математика