Ромб. Периметр ромба

Ромб – это четырехугольник, у которого все четыре стороны равны между собой. Эта геометрическая фигура имеет множество интересных свойств и характеристик, а ее периметр является одним из ключевых параметров, который позволяет оценить длину контура ромба.

Основные свойства ромба

1. Стороны равны: В ромбе все четыре стороны имеют одинаковую длину. Обозначим эту длину как “a”.
2. Углы ромба: Углы ромба также равны между собой и составляют 90 градусов.
3. Диагонали ромба: Диагонали ромба пересекаются под прямым углом и делят его на четыре равных треугольника. Обозначим длины диагоналей как “d₁” и “d₂“.
4. Свойство серединных перпендикуляров: Диагонали ромба также являются серединными перпендикулярами к его сторонам. Это означает, что каждая диагональ делит ромб на два равных треугольника.

Периметр ромба

Периметр ромба – это сумма длин всех его сторон. Для ромба с равными сторонами “a”, периметр можно выразить двумя разными способами:

1. Через сторону

Периметр ромба по формуле через сторону выглядит следующим образом:

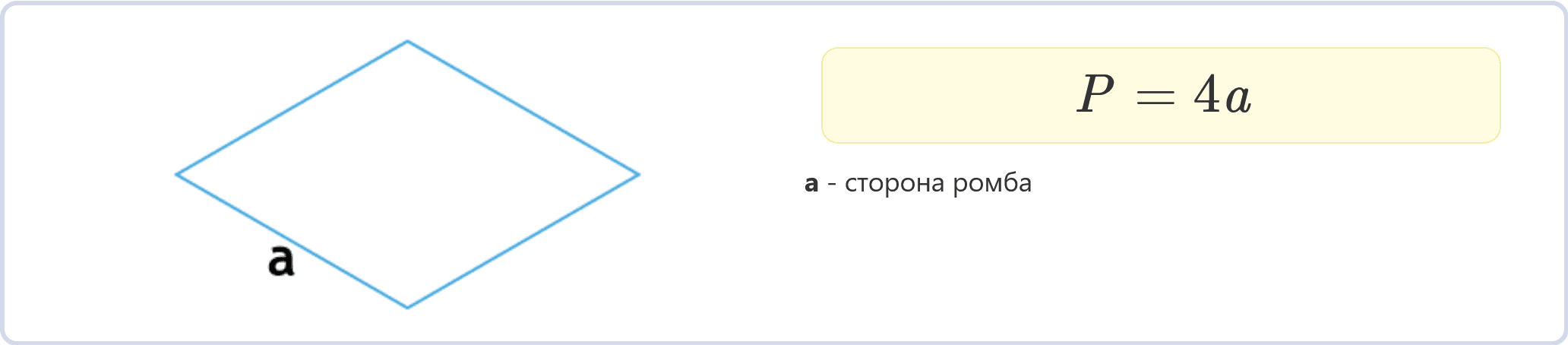
P = 4a

a – сторона ромба

Через диагонали

Также можно выразить периметр ромба через диагонали:

P = 2√d₁​² + d_2​²​

d₁ и d_2​ – диагонали ромба

Практическое применение

Ромбы встречаются в различных областях, включая геометрию, архитектуру, дизайн и инженерию. Знание свойств ромба и формул для расчета его периметра может быть полезным при решении задач, связанных с расположением и измерением объектов, имеющих форму ромба.

Заключение

Ромб – это геометрическая фигура с уникальными свойствами, обладающая симметрией и равными углами. Расчет периметра ромба позволяет оценить длину его контура и может быть использован в различных областях, где ромбы играют важную роль.

Полезен ли материал?

ДаНет

5 / 6

#Калькуляторы #Математика