Используйте этот калькулятор для быстрого расчета числа сочетаний и решения различных задач, связанных с выбором элементов из множества!
Число сочетаний: формула и как найти
Число сочетаний – важное понятие в комбинаторике, которое описывает количество способов выбрать k элементов из n элементов без учета порядка. Это число часто используется в различных областях, таких как теория вероятностей, статистика и информатика.
Формула для расчета числа сочетаний
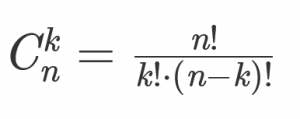
Формула для расчета числа сочетаний имеет вид:
C(n, k) = n! / (k! * (n - k)!)
Где:
n!– факториал числа n, равный произведению всех положительных целых чисел от 1 до n.k!– факториал числа k.
Читается обозначение следующим образом – “C из n по k“.
Как найти число сочетаний
Для расчета числа сочетаний по формуле, следуйте этим шагам:
- Определите значения n (общее количество элементов) и k (количество элементов, которые вы хотите выбрать).
- Вычислите факториалы для n, k и (n – k).
- Подставьте значения в формулу числа сочетаний и произведите вычисления.
Число сочетаний: Где и для чего используется
Число сочетаний является важным понятием в математике, особенно в области комбинаторики. Это число широко применяется в различных научных и практических областях. Давайте рассмотрим, где и для чего используется число сочетаний.
1. Комбинаторика и Теория Вероятностей:
- Распределение вероятностей: Число сочетаний используется при решении задач вероятности, особенно в ситуациях, где важен порядок выбора элементов.
- Сочетания без повторений: В комбинаторике, число сочетаний применяется для определения количества способов выбрать k элементов из n элементов, где порядок не имеет значения.
2. Статистика и Исследования:
- Выборки и обследования: При проведении исследований и выборочных обследований, число сочетаний помогает определить количество различных комбинаций выборок из большого множества.
3. Информатика и Компьютерные науки:
- Комбинаторные алгоритмы: В информатике, число сочетаний используется при проектировании алгоритмов, основанных на комбинаторных принципах.
- Криптография: В некоторых сценариях криптографии, комбинаторные принципы используются для обеспечения безопасности систем.
4. Финансы и Бизнес:
- Финансовый анализ: В финансах число сочетаний может использоваться для определения возможных комбинаций портфеля инвестиций.
- Бизнес-прогнозирование: При прогнозировании различных сценариев развития бизнеса, число сочетаний может помочь в оценке вариантов выбора.
5. Образование:
- Математическое обучение: Число сочетаний является важной темой в образовании, и его изучение способствует развитию навыков комбинаторного мышления.
- Задачи на логику: Число сочетаний используется в учебных задачах, проверяющих логическое мышление студентов.
6. Игровая индустрия:
- Генерация уровней: В разработке компьютерных игр число сочетаний может использоваться для генерации различных уровней или вариаций геймплея.
Число сочетаний – это мощный математический инструмент, который находит свое применение в различных областях. Понимание его принципов и использование формулы расчета позволяет решать разнообразные задачи, связанные с выбором элементов из множества, и анализировать различные комбинаторные сценарии.
Пример нахождения числа сочетаний
Задача 1: Лотерея “5 из 36”
Рассмотрим лотерею “5 из 36” и найдем количество возможных комбинаций.
Решение
Используем формулу для числа сочетаний:
C(n, k) = n! / (k! * (n - k)!)
В данной задаче:
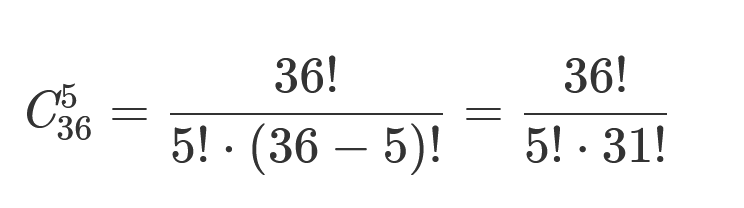
Подставляем значения и упрощаем:
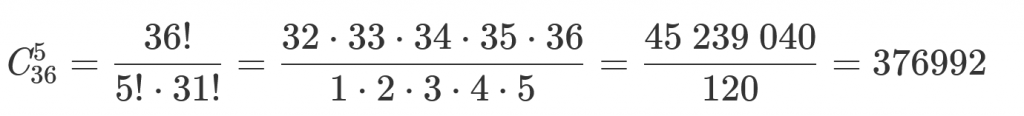
Ответ: В лотерее “5 из 36” существует 376,992 возможных комбинации.
Полезен ли материал?
10 / 1

