Число перестановок. Калькулятор и формула
Число перестановок – это основное понятие в комбинаторике, которое играет важную роль в различных областях науки, инженерии и информатики. В этой статье мы рассмотрим, что такое число перестановок, как его вычислить, и где оно находит свое практическое применение.
Число перестановок: Обзор, Формула и Практическое Применение
Число перестановок представляет собой количество способов упорядочивания элементов набора. Это количество различных способов, которыми можно расположить элементы без повторений. Если у нас есть набор из n уникальных элементов, то число перестановок для этого набора будет n! (n факториал).
Формула для вычисления числа перестановок
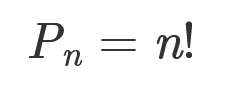
Формула для числа перестановок n элементов (n!):
\[ n! = n \cdot (n-1) \cdot (n-2) \cdot … \cdot 3 \cdot 2 \cdot 1 \]
Например, если у нас есть 4 уникальных элемента, число перестановок будет:
\[ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 \]
Число перестановок: практическое применение
- Комбинаторика и Теория Вероятностей: Число перестановок играет важную роль в комбинаторике и теории вероятностей. Например, при решении задач на распределение карточных комбинаций в покере или определении числа возможных порядковых комбинаций событий.
- Информатика и Алгоритмы: В информатике число перестановок часто используется при анализе алгоритмов и структур данных. Это может быть важным параметром при оптимизации алгоритмов сортировки, поиска и других операций над данными.
- Математическое Моделирование: В математическом моделировании число перестановок может быть использовано для анализа различных систем и вариантов их упорядочения. Это может быть полезно, например, при исследовании возможных вариантов распределения ресурсов.
- Криптография: В криптографии число перестановок может быть использовано для создания различных ключей шифрования и обеспечения безопасности информации.
Заключение
Число перестановок – это важное математическое понятие, нашедшее свое применение в различных областях науки и техники. Оно позволяет оценивать количество возможных упорядочиваний элементов в наборе и широко применяется в комбинаторике, теории вероятностей, информатике и других областях. Понимание этого понятия является ключом к решению различных задач, связанных с анализом вариантов и возможностей.
Полезен ли материал?
4 / 2


