Разложение числа на простые множители

Разложение числа на простые множители – это фундаментальный математический процесс, который позволяет представить любое число как произведение простых чисел. Эта техника, известная также как факторизация, играет важную роль в различных областях математики и находит свое применение в решении разнообразных задач.

Основные понятия

Простые числа – это натуральные числа, большие единицы, которые имеют только два делителя: единицу и само число. Примеры простых чисел включают 2, 3, 5, 7, 11 и так далее. Разложение числа на простые множители заключается в представлении этого числа как произведения простых множителей.

Процесс разложения

1. Выбор начального числа: Возьмем натуральное число, которое мы хотим разложить.
2. Нахождение простых делителей: Начнем делить число на наименьшие простые числа, начиная с 2. Если число делится на 2, то 2 становится первым простым множителем. Если нет, то переходим к следующему простому числу и так далее.
3. Продолжение деления: Процесс деления продолжается, пока число не станет равным 1. Каждый раз, когда число делится на простое число, оно заменяется результатом деления, и в результате формируется список простых множителей.
4. Составление произведения: Полученные простые множители умножаются между собой, и в итоге получается разложение исходного числа.

Пример разложения числа на простые множители

Рассмотрим подробно разложение числа 36 на простые множители:

Начнем с деления на 2. Так как 36 делится на 2 без остатка, первым простым множителем будет 2.

36 : 2 = 18

Теперь рассмотрим оставшееся число 18. Продолжим делить его на 2.

18 : 2 = 9

Рассматриваем оставшееся число 9 и делим его на следующий простой множитель, который также является 3.

9 : 3 = 3

Теперь число 3 не делится больше ни на какие простые числа, так как само является простым числом.

3 = 3

Объединим все полученные простые множители:

36 = 2 × 2 × 3 × 3

Или более компактно:

36 = 22 × 32

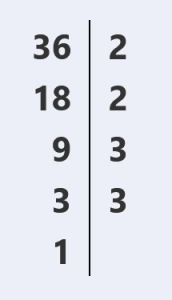
Ответ: 36 = 2 × 2 × 3 × 3

Практическое применение

1. Шифрование: Разложение на простые множители используется в криптографии для создания шифров, таких как RSA, где безопасность основана на сложности факторизации больших чисел.
2. Математические задачи: Факторизация применяется в решении уравнений, нахождении наименьшего общего кратного, а также в других математических задачах.
3. Оптимизация кода: В информатике разложение чисел на простые множители может быть использовано для оптимизации кода и ускорения выполнения некоторых алгоритмов.

В заключение, разложение числа на простые множители является важным инструментом в мире математики, науки и технологий. Понимание этого процесса позволяет решать разнообразные задачи и создавать эффективные алгоритмы в различных областях.

Полезен ли материал?

ДаНет

5 / 7

#Калькуляторы #Математика