На данной странице вы можете легко рассчитать координаты середины отрезка как на плоскости, так и в трехмерном пространстве. Просто введите координаты начальной и конечной точек, и наш онлайн-калькулятор предоставит вам ответ, а также подробное описание вычислений.

Задача на поиск координат середины отрезка часто встречается в геометрии и других областях. Наш сайт предоставляет возможность рассчитать длину отрезка, заданного его координатами.

Координаты середины отрезка

Отрезок – это часть прямой линии между двумя точками. В геометрии, нахождение середины отрезка имеет важное значение, как на плоскости, так и в трехмерном пространстве. Эта операция позволяет нам определить точку, которая равноудалена от двух концов отрезка. Для нахождения координат середины отрезка существуют специальные формулы.

Координаты середины отрезка на плоскости

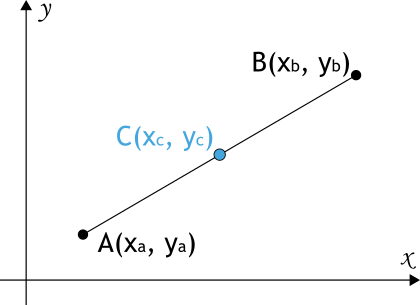
На плоскости для нахождения координат середины отрезка (точка C), соединяющего две точки A(x_a, y_a) и B(x_b, y_b), используется следующая формула:

x_c = (x_a + x_b) ÷ 2

y_c = (y_a + y_b) ÷ 2

x_a и y_a – координаты первой точки A,

x_b и y_b – координаты второй точки B,

x_c и y_c – координаты середины отрезка (точка C).

Эти формулы просты и позволяют быстро найти середину отрезка на плоскости. Они работают для отрезков, горизонтальных, вертикальных и наклонных.

Координаты середины отрезка в пространстве

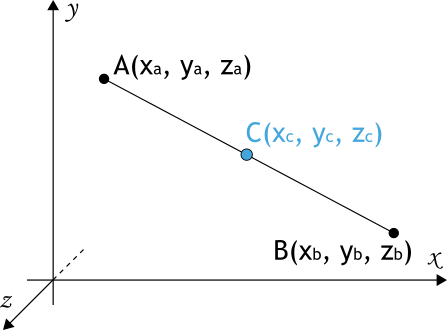
В трехмерном пространстве для нахождения координат середины отрезка (точка C) между двумя точками A(x_a, y_a, z_a) и B(x_b, y_b, z_b) используются аналогичные формулы:

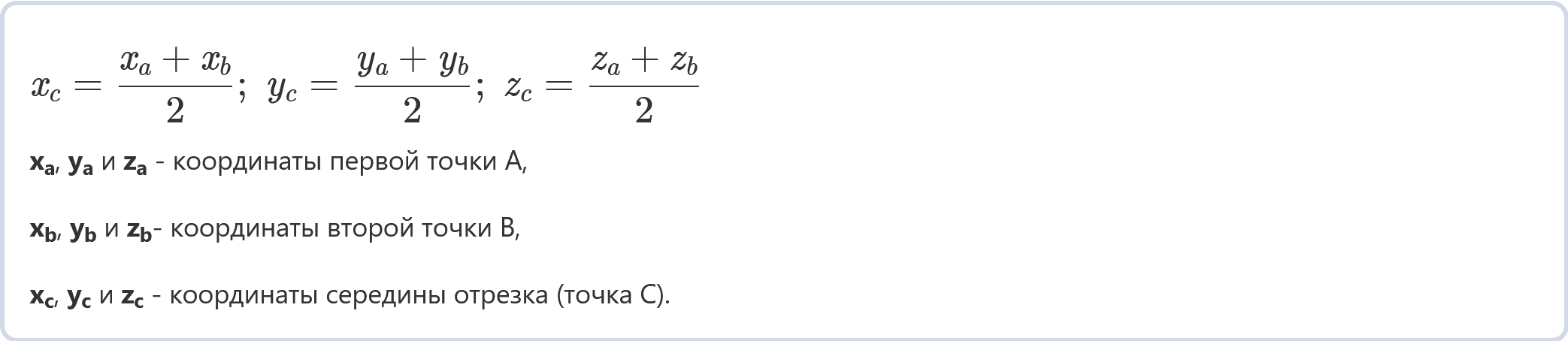
x_c = (x_a + x_b) ÷ 2

y_c = (y_a + y_b) ÷ 2

z_c = (z_a + z_b) ÷ 2

x_a, y_a и z_a – координаты первой точки A,

x_b, y_b и z_b – координаты второй точки B,

x_c, y_c и z_c – координаты середины отрезка (точка C).

Эти формулы аналогичны формулам на плоскости и также позволяют найти середину отрезка между двумя точками.

Где используется нахождение середины отрезка?

Нахождение середины отрезка находит применение в различных областях и задачах:

1. Геометрия: Это фундаментальное понятие в геометрии, и оно используется для вычисления расстояний, углов, и других характеристик между точками и отрезками.
2. Компьютерная графика: При построении графики и моделировании 3D объектов часто требуется находить середины отрезков для корректного отображения объектов.
3. Инженерия и архитектура: В строительстве и дизайне конструкций необходимо находить середины отрезков для расчетов и построения планов.
4. Программирование: В разработке программного обеспечения нахождение середины отрезков может потребоваться при решении геометрических задач или для оптимизации алгоритмов.

В заключение, нахождение координат середины отрезка – это фундаментальная задача в математике и геометрии, которая находит широкое применение в различных областях, включая инженерию, архитектуру, компьютерную графику и программирование. Формулы для нахождения середины отрезка на плоскости и в пространстве позволяют эффективно решать задачи, связанные с этой операцией.

Калькулятор координат середины отрезка

Для удобного расчета координат середины отрезка на плоскости и в трехмерном пространстве вы можете использовать специальный калькулятор.

Этот инструмент поможет вам быстро определить точку C – середину отрезка, используя координаты точек A и B.

Просто выберите тип отрезка (2D или 3D), введите координаты точек A и B, и калькулятор автоматически выполнит расчет.

Результат будет представлен в виде координат X, Y и при необходимости Z.

Полезен ли материал?

ДаНет

2 / 0

#Калькуляторы #Математика