Площади поверхности цилиндра
Цилиндр – одна из самых фундаментальных геометрических фигур, которая присутствует в повседневной жизни и находит широкое применение в различных областях, от строительства до инженерии. В данной статье мы рассмотрим структуру цилиндра, определим его площадь поверхности и рассмотрим некоторые интересные свойства этой удивительной фигуры.
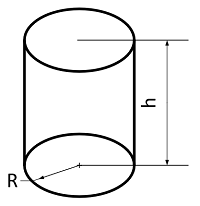
Структура цилиндра
Цилиндр – трехмерная геометрическая фигура, которая состоит из двух параллельных и равных окружностей, называемых основаниями, и боковой поверхности, которая представляет собой прямоугольный параллелепипед, образованный путем соединения соответствующих точек окружностей оснований. Основания цилиндра имеют равные радиусы, и линия, проходящая через центры этих окружностей, называется осью цилиндра.
Площадь поверхности цилиндра
Чтобы найти площадь поверхности цилиндра, нужно рассмотреть его составные части: площадь боковой поверхности и две площади оснований.
Площадь боковой поверхности (Sбок)

Боковая поверхность цилиндра представляет собой прямоугольный параллелепипед, у которого одна из сторон является окружностью, а другая – высота цилиндра (h). Таким образом, площадь боковой поверхности вычисляется по формуле:
Sбок = 2 * π * r * h
где π (пи) – математическая константа, приближенно равная 3.14159, r – радиус основания цилиндра, h – высота цилиндра.
Площадь оснований (Sосн)
Каждое из оснований цилиндра – это окружность с радиусом (r), и площадь одного основания вычисляется по формуле:
Sосн = π * r2
Общая площадь поверхности цилиндра (S)

Формула 1:
S = 2πR(h + R)
Здесь “S” – площадь поверхности, “R” – радиус основания цилиндра, а “h” – высота цилиндра.
Формула 2:
Общая площадь поверхности цилиндра (S) – это сумма площади боковой поверхности и двух площадей оснований:
S = 2 * π * r * h + 2 * π * r2
Обе формулы описывают площадь поверхности цилиндра. В первой формуле “S” представляет общую площадь поверхности цилиндра, включая его боковую поверхность и два круглых основания. Во второй формуле “S” представляет общую площадь поверхности, разбитую на две части: боковую поверхность и два круглых основания.
Таким образом, обе формулы равнозначны и могут быть использованы для вычисления площади поверхности цилиндра, в зависимости от того, какая информация вам известна. Если известны радиус “R” и высота “h” цилиндра, то можно использовать первую формулу, а если известны радиус “r” и высота “h”, то можно использовать вторую.
Применение цилиндров
Цилиндры имеют широкое применение в различных областях науки, техники и повседневной жизни. Вот несколько примеров:
- Трубопроводы: Множество трубопроводов, используемых для транспортировки жидкостей и газов, имеют форму цилиндра.
- Бутыли и банки: Многие контейнеры для хранения жидкостей и продуктов обладают формой цилиндра.
- Колонны и столбы: Многие архитектурные элементы и сооружения имеют форму цилиндра.
- Валы и цилиндрические ролики: В технике широко используются цилиндрические формы для передачи движения и снижения трения.
Интересные свойства цилиндра
- Все цилиндры являются поверхностями вращения, то есть образованы вращением прямоугольника вокруг одной из своих сторон.
- Объем цилиндра (V) определяется по формуле: V = π * r2 * h, где r – радиус основания, h – высота.
- Цилиндр является примером кругового цилиндра, у которого оба основания параллельны и имеют одинаковый размер, и прямого цилиндра, у которого основания перпендикулярны к боковой поверхности.
- Каждая точка на боковой поверхности цилиндра находится на одинаковом расстоянии от его оси.
Цилиндры – уникальные и полезные геометрические фигуры, которые имеют важное практическое применение и обладают интересными свойствами. Их площадь поверхности и объем играют важную роль в различных инженерных расчетах и конструкциях, делая их неотъемлемой частью нашей современной жизни.
Полезен ли материал?
1 / 0


