Куб: определение, свойства и вычисление площади поверхности
Определение и свойства куба
Куб – это геометрическое тело, являющееся одним из пяти правильных многогранников в трехмерном пространстве.
Куб обладает следующими особенностями:
- Все его грани являются квадратами.
- У всех граней равные стороны.
- Все углы между гранями равны 90 градусам.
- У куба 12 ребер, 8 вершин и 6 граней.
Площадь полной поверхности куба
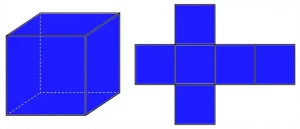
Площадь полной поверхности куба обозначается как Sполн. Куб имеет шесть граней, и площадь каждой грани равна a2, где a – длина ребра куба. Таким образом, чтобы вычислить площадь полной поверхности куба, необходимо сложить площади всех его граней.
Существует несколько способов вычисления площади полной поверхности куба, в зависимости от известных параметров:
Через ребро
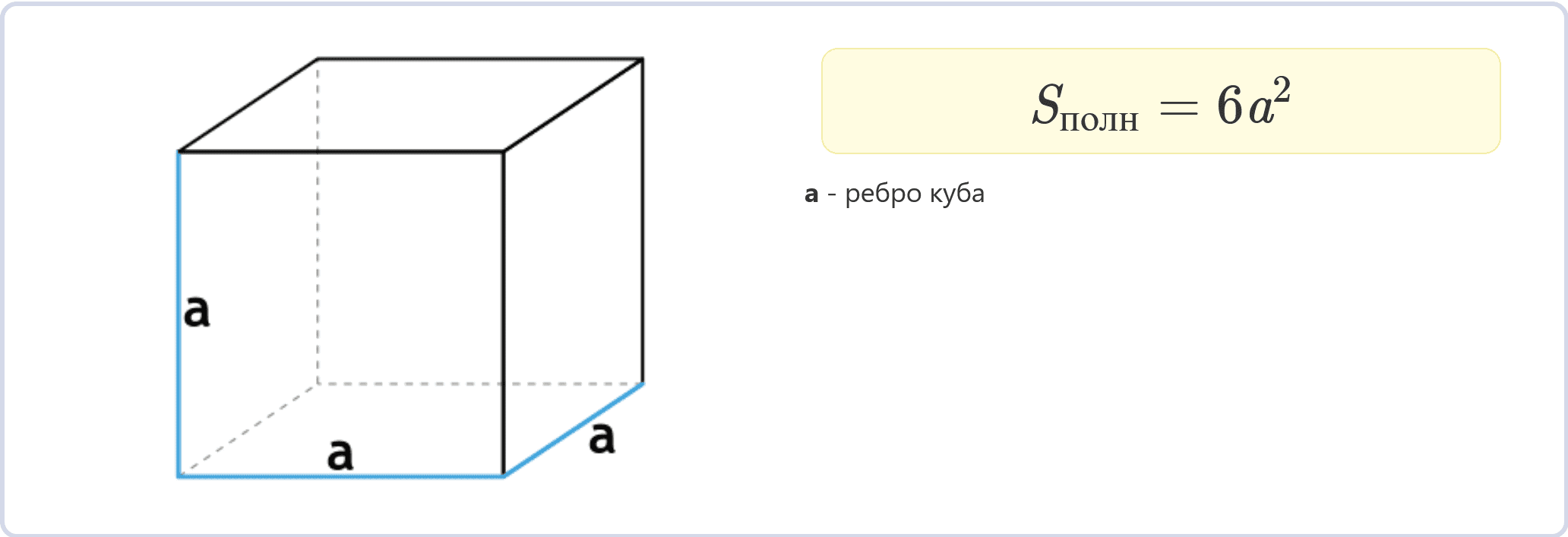
Sполн = 6a2
Это самый простой способ вычисления площади полной поверхности куба, если известна длина его ребра a.
Через диагональ грани
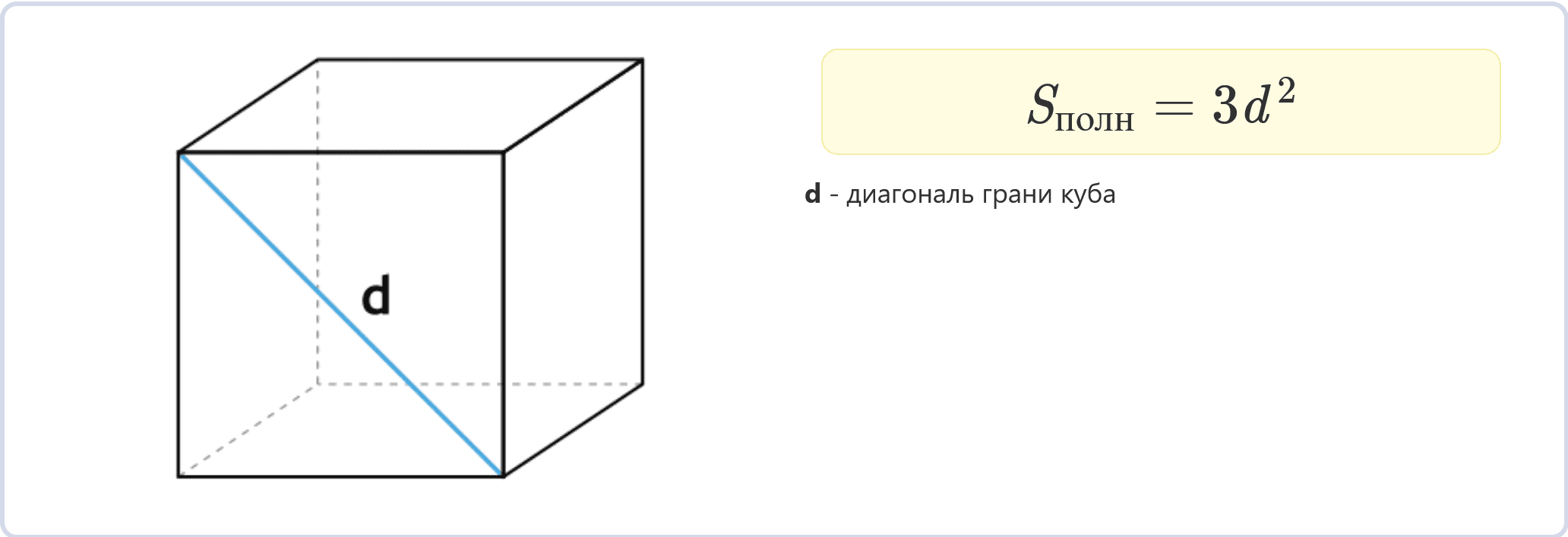
Sполн = 3d2
Если известна длина диагонали d одной грани куба, то площадь полной поверхности можно найти, используя эту формулу.
Через диагональ куба
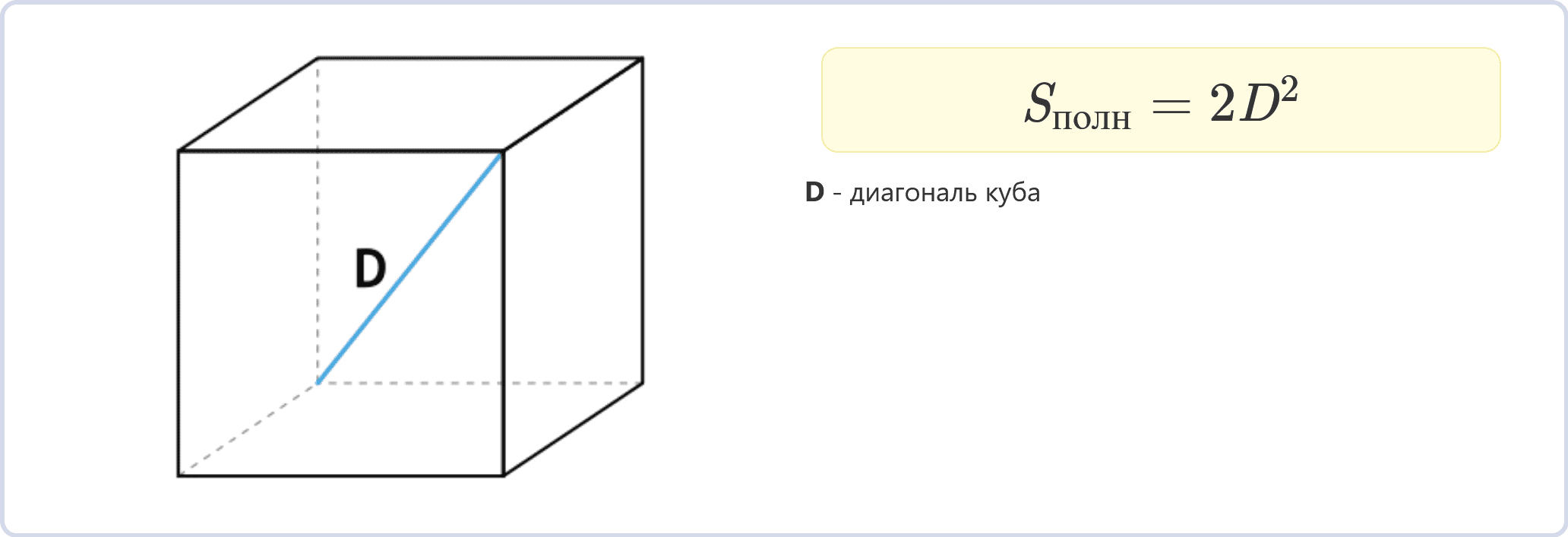
Sполн = 2D2
Если известна длина диагонали D куба (расстояние между двумя противоположными вершинами), можно вычислить площадь полной поверхности.
Через периметр грани
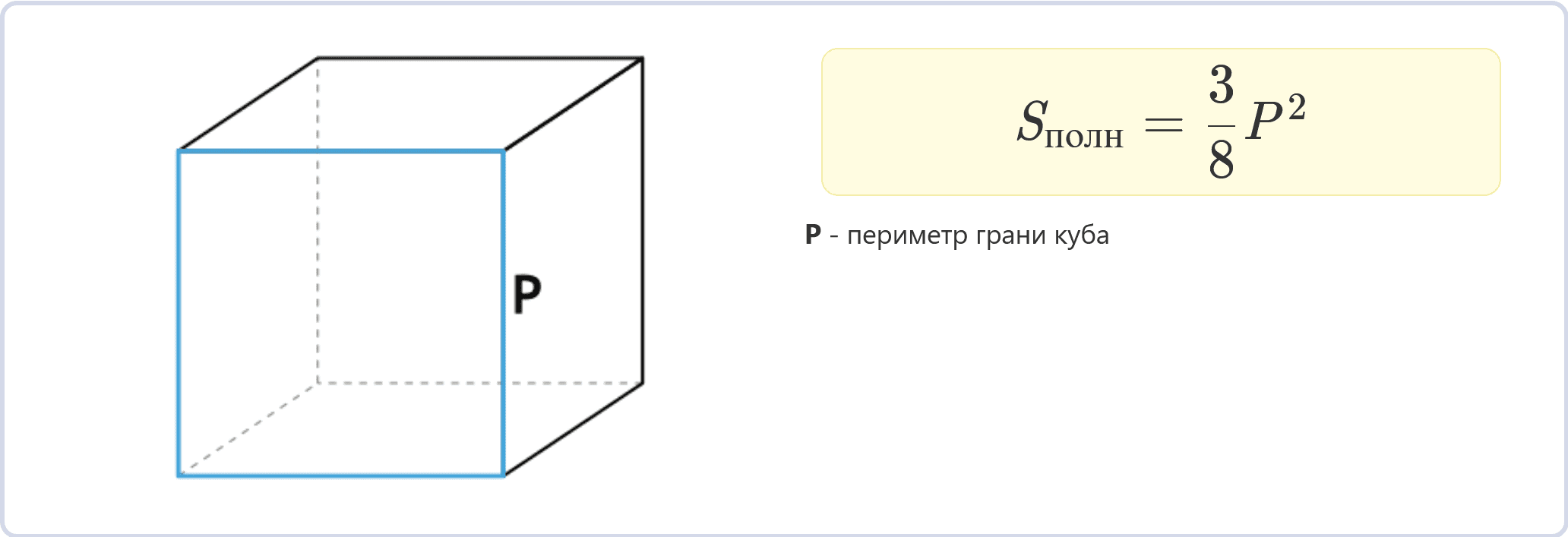
Sполн = (3/8)P2
Если известен периметр P одной грани куба, площадь полной поверхности можно найти по этой формуле.
Через периметр куба
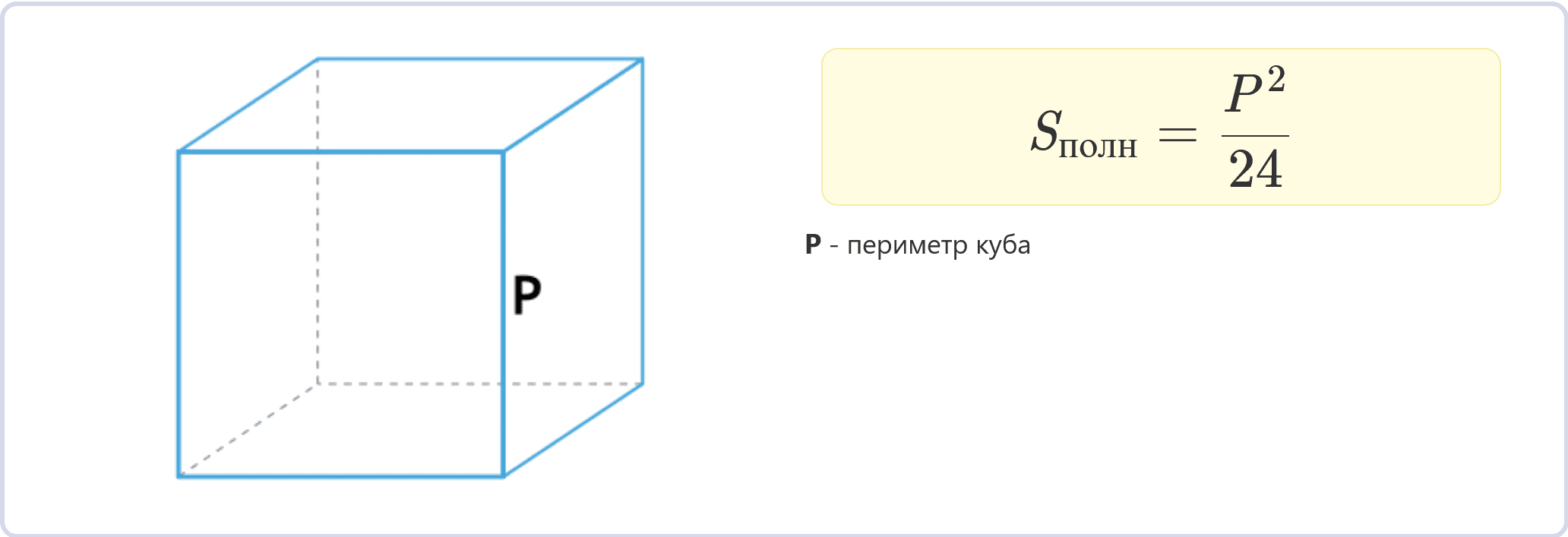
Sполн = (P2)/24
Если известен периметр P куба (сумма длин всех его ребер), можно вычислить площадь полной поверхности.
Через объем
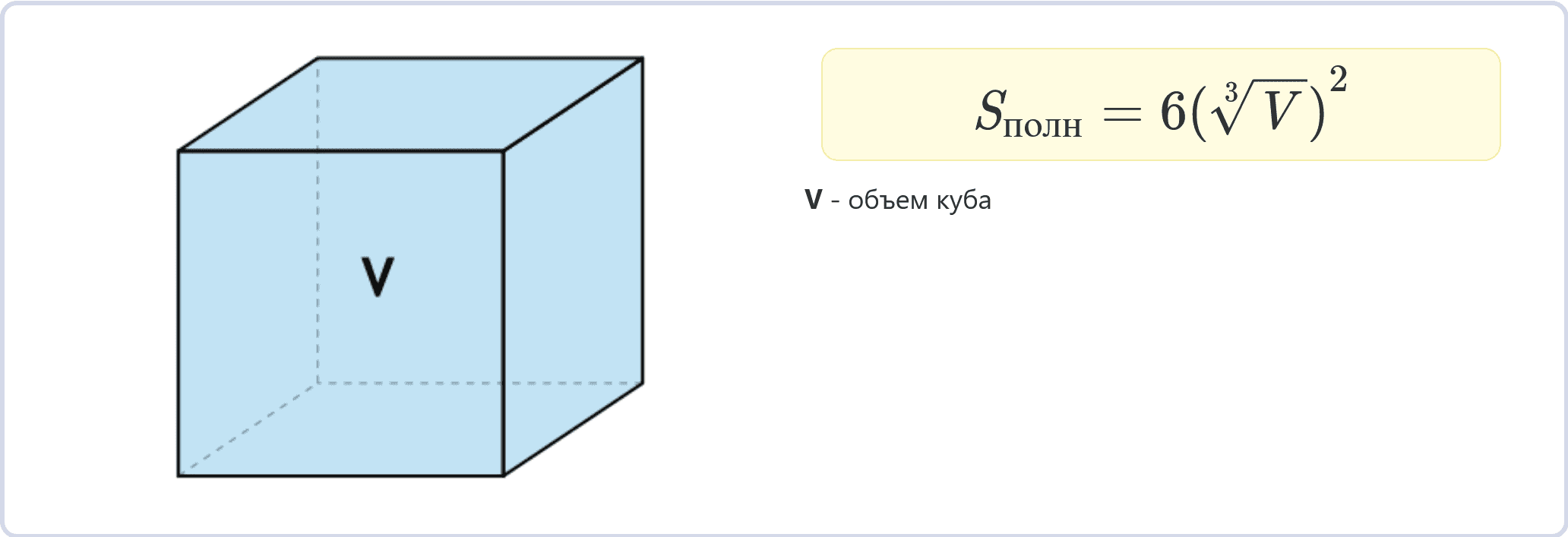
Sполн = 6 * (3√V)2
Если известен объем V куба, площадь полной поверхности может быть найдена с помощью этой формулы.
Через площадь вписанного шара
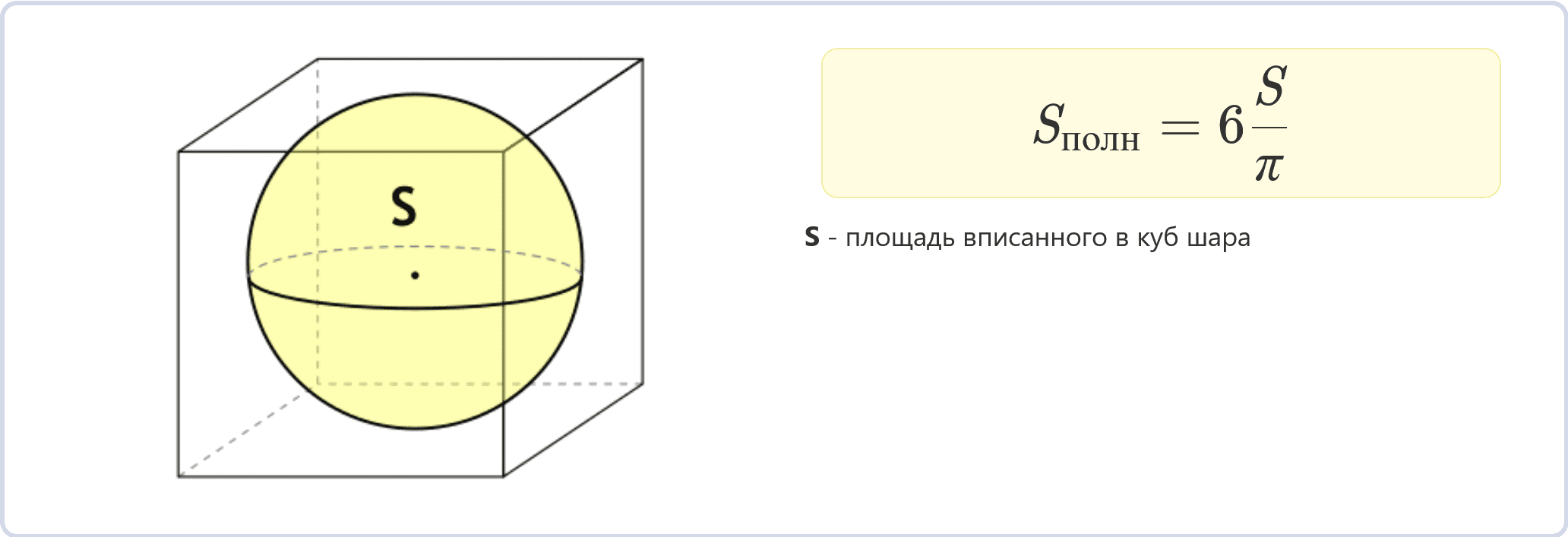
Sполн = 6(S/π)
Если известна площадь S вписанного в куб шара, то площадь полной поверхности куба можно вычислить с помощью этой формулы.
Площадь боковой поверхности куба
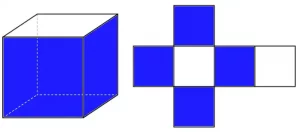
Площадь боковой поверхности куба обозначается как Sбок. Боковые грани куба являются квадратами, и площадь каждой боковой грани равна a2, где a – длина ребра куба.
Существует несколько способов вычисления площади боковой поверхности куба, в зависимости от известных параметров:
Через ребро
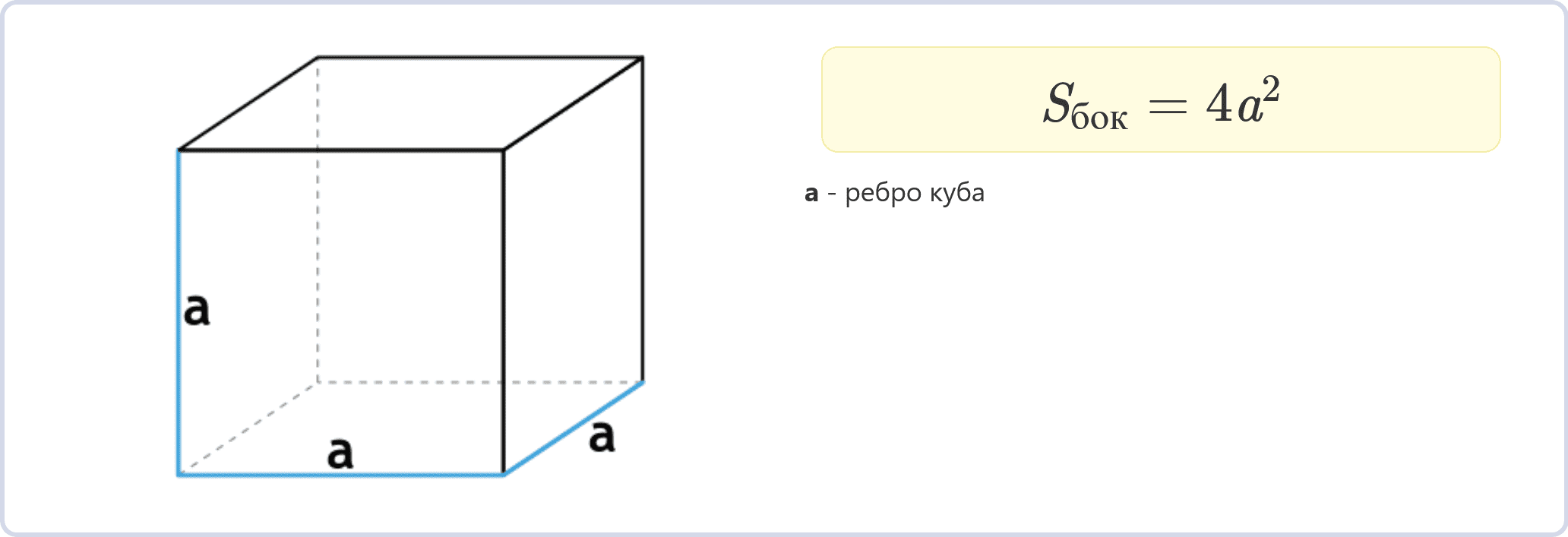
Sбок = 4a2
Это простейший способ вычисления площади боковой поверхности куба, если известна длина его ребра a.
Через диагональ грани
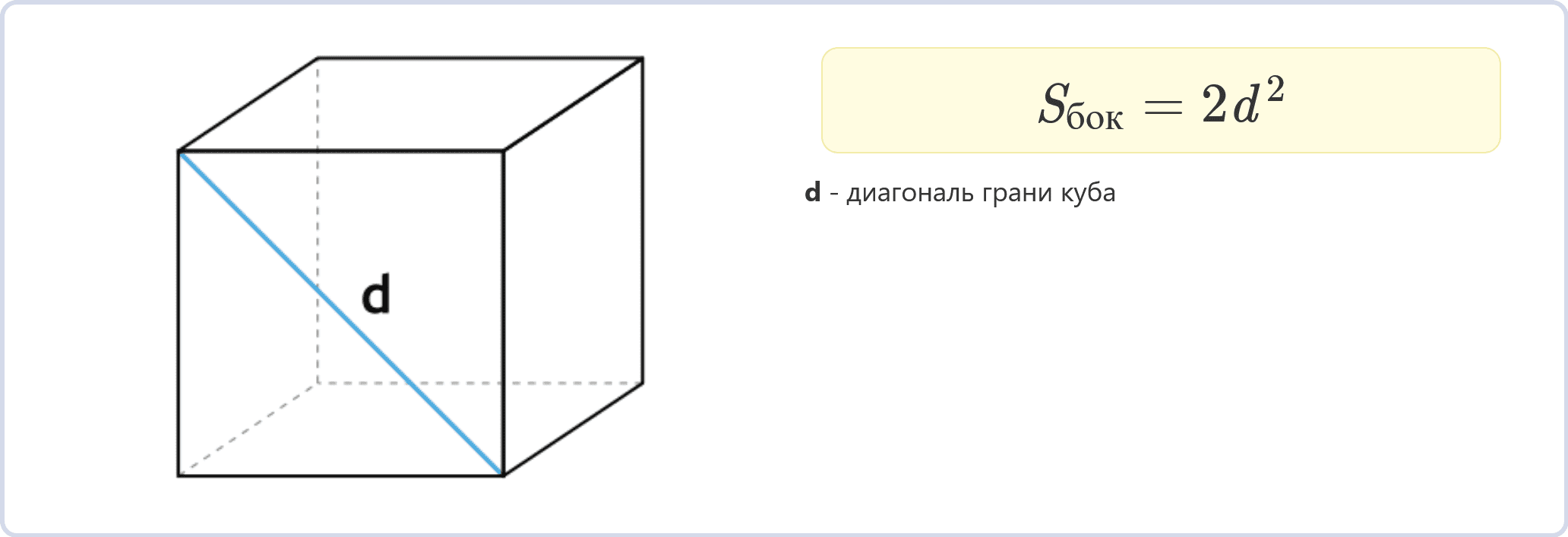
Sбок = 2d2
Если известна длина диагонали d одной грани куба, то площадь боковой поверхности можно найти, используя эту формулу.
Через диагональ куба
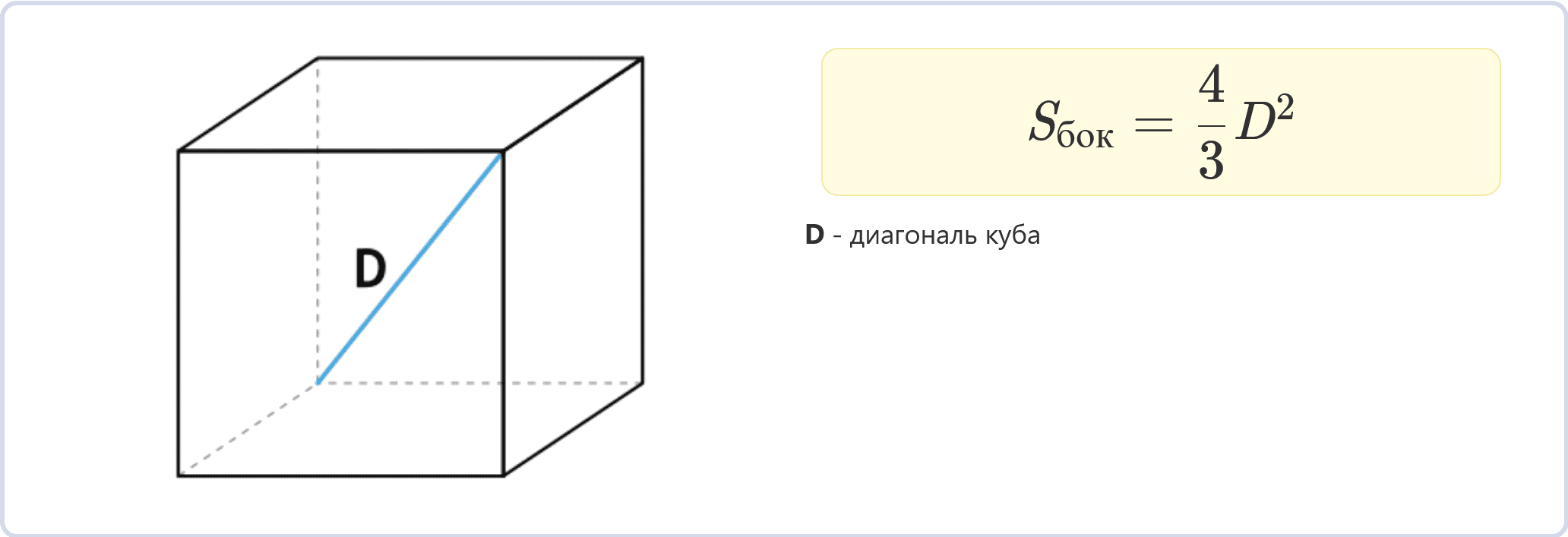
Sбок = (4/3)D2
Если известна длина диагонали D куба (расстояние между двумя противоположными вершинами), можно вычислить площадь боковой поверхности.
Через периметр грани
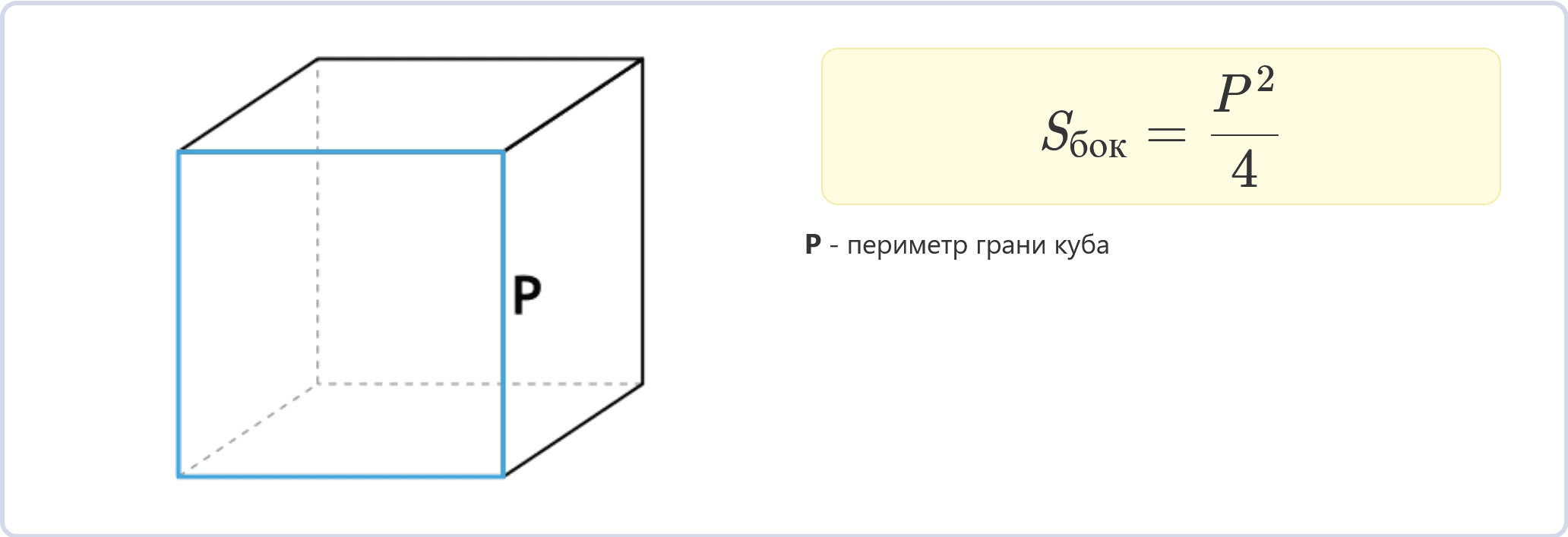
Sбок = (P2)/4
Если известен периметр P одной грани куба, площадь боковой поверхности можно найти по этой формуле.
Через периметр куба
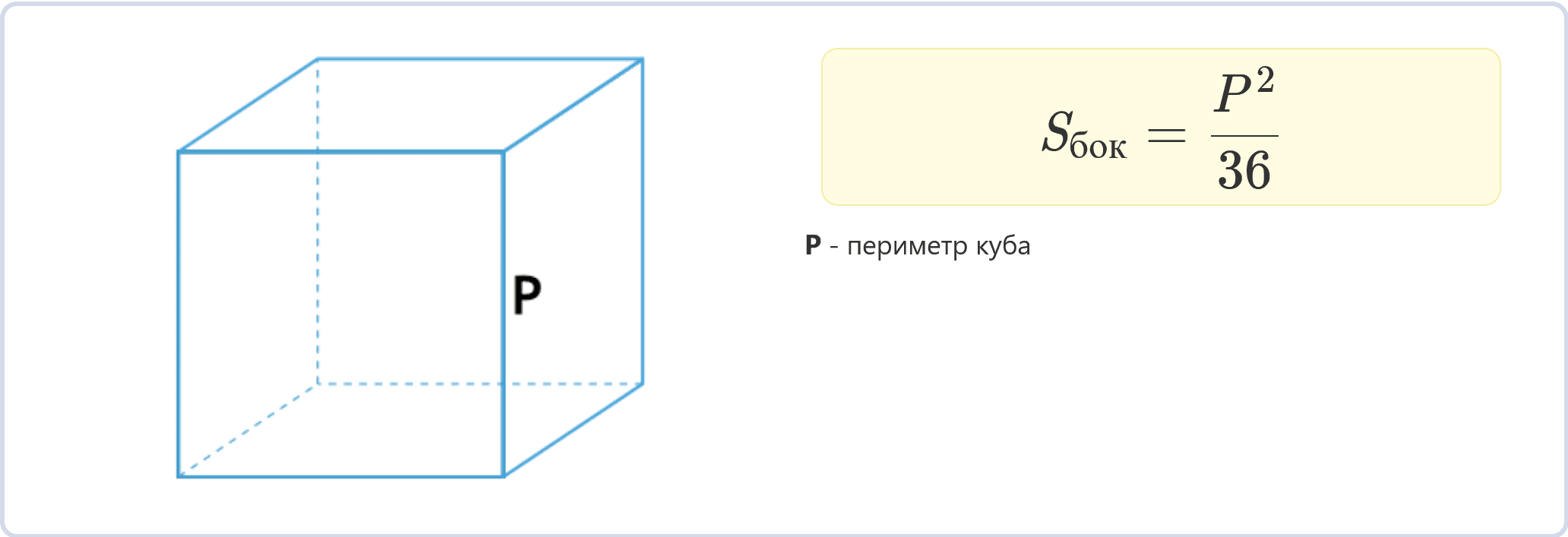
Sбок = (P2)/36
Если известен периметр P куба (сумма длин всех его ребер), можно вычислить площадь боковой поверхности.
Через объем

Sбок = 4 * (3√V)2
Если известен объем V куба, площадь боковой поверхности может быть найдена с помощью этой формулы.
Таким образом, площадь полной поверхности и площадь боковой поверхности куба могут быть легко вычислены с использованием соответствующих формул в зависимости от известных параметров. Куб – одно из самых интересных и важных геометрических тел, широко применяемых в различных областях науки и техники.
Полезен ли материал?
2 / 0


