Параллелограмм: свойства и формулы

Параллелограмм – это особый вид четырехугольника, в котором противоположные стороны параллельны друг другу. Это одна из важнейших фигур в геометрии, которая обладает множеством уникальных свойств и формул. В данной статье мы рассмотрим основные характеристики параллелограмма, его площадь и предоставим примеры использования в реальной жизни.

Основные свойства параллелограмма:

1. Параллельные стороны: У параллелограмма противоположные стороны параллельны. Это означает, что если две стороны параллелограмма одновременно пересекаются с прямой, то остальные две стороны также пересекут эту прямую.
2. Равные противоположные углы: У параллелограмма противоположные углы равны между собой. Это означает, что если один из углов параллелограмма равен, например, 60 градусов, то его противоположный угол тоже будет равен 60 градусов.
3. Диагонали: Диагонали параллелограмма делят его на две равные части и пересекаются в точке, которая делит каждую из них пополам. Таким образом, диагонали являются осью симметрии параллелограмма.
4. Противоположные стороны равны: У параллелограмма противоположные стороны равны по длине. Это следует из его определения как фигуры с параллельными сторонами.
5. Смежные углы дополнительны: Смежные углы параллелограмма дополнительны друг к другу. Это означает, что сумма двух смежных углов всегда составляет 180 градусов.

Площадь параллелограмма:

Площадь параллелограмма можно вычислить различными способами, в зависимости от того, какие данные о нем известны. Вот несколько формул для вычисления площади параллелограмма через различные параметры:

Через длину основания и высоту

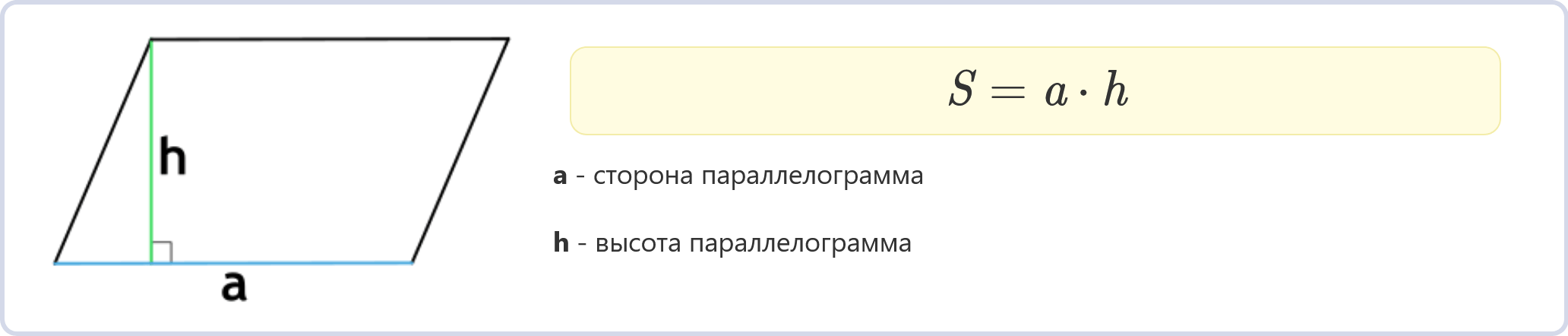
S = a * h

Площадь параллелограмма равна произведению длины одной из его оснований (a) на длину высоты (h), проведенной к этому основанию.

Через длины двух сторон и угол между ними

S = a * b * sin(α)

Площадь параллелограмма равна произведению длин двух его сторон (a и b) на синус угла (α) между этими сторонами.

Через длины двух диагоналей и угол между ними

S = (d₁* d₂ * sin($\alpha$)) / 2

Площадь параллелограмма равна половине произведения длин его диагоналей (d₁ и d₂) на синус угла ($\alpha$) между ними.

Площадь параллелограмма: примеры использования

1. Строительство и архитектура: В строительстве и архитектуре параллелограммы часто используются для создания крыш и фундаментов зданий.
2. Геодезия: В геодезии параллелограммы применяются для измерения углов и определения расстояний между точками.
3. Инженерия: В различных областях инженерии, таких как машиностроение и электротехника, параллелограммы могут быть использованы для моделирования и проектирования различных конструкций и механизмов.
4. Игры: В некоторых настольных играх и головоломках используются параллелограммы для создания интересных геометрических фигур.
5. Естественные явления: Некоторые естественные явления, такие как образование кристаллов и ледниковых образований, также могут быть описаны с помощью параллелограммов.

Параллелограммы имеют широкий спектр применений и важны в различных областях. Изучение их свойств и формул позволяет решать разнообразные задачи, связанные с этими фигурами, и углублять понимание геометрии в целом.

 

Полезен ли материал?

ДаНет

1 / 1

#Калькуляторы #Математика #Площадь