Объем шара
Объем шара – это объем трехмерной фигуры, которая имеет форму сферы. Шар является одним из наиболее известных геометрических объектов и имеет ряд интересных свойств. Рассмотрим, как можно вычислить объем шара с использованием различных формул и какой калькулятор можно использовать для этой цели.
Формула объема шара через радиус
Наиболее распространенным и простым способом вычисления объема шара является использование его радиуса. Формула для объема шара через радиус выглядит следующим образом:
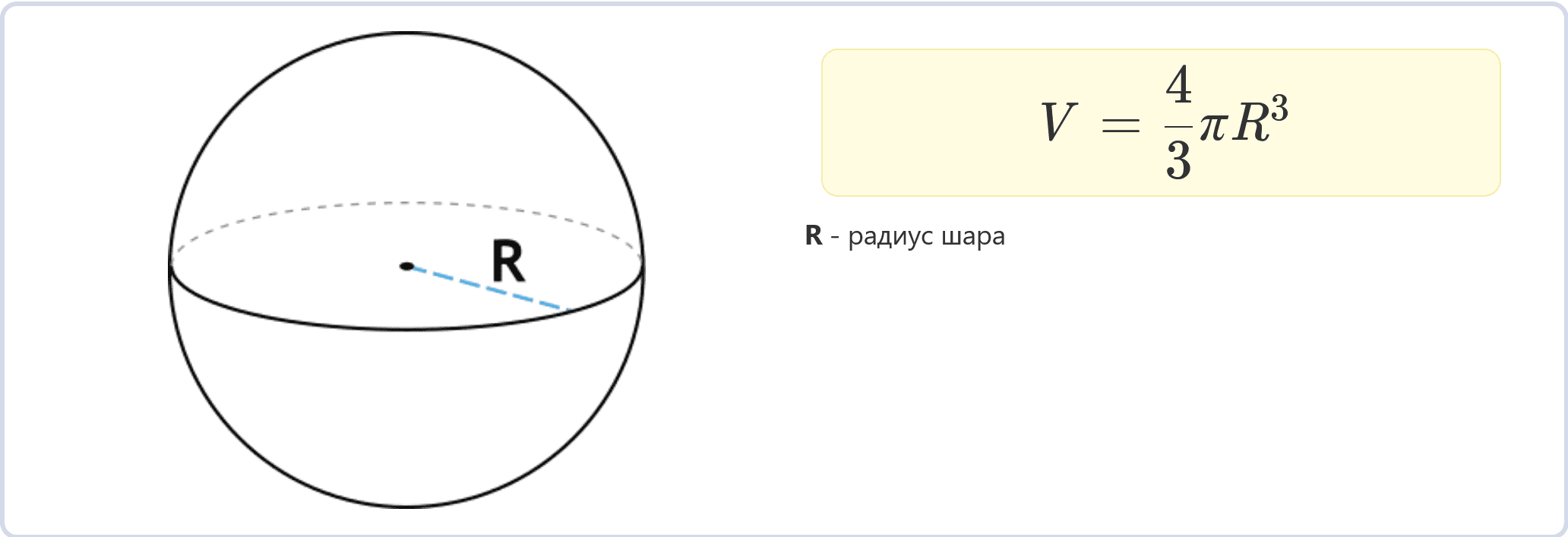
\(V = \dfrac{4}{3} \pi R^3\)
V – объем шара,
π (пи) – математическая константа, приближенно равная 3.14159,
R – радиус шара.
Чтобы вычислить объем шара с использованием этой формулы, достаточно знать его радиус. Просто подставьте значение радиуса в формулу и выполните вычисления.
Формула объема шара через диаметр
Диаметр шара – это расстояние от одной стороны шара до противоположной стороны, проходящее через его центр. Если известен диаметр, то объем шара можно вычислить следующим образом:
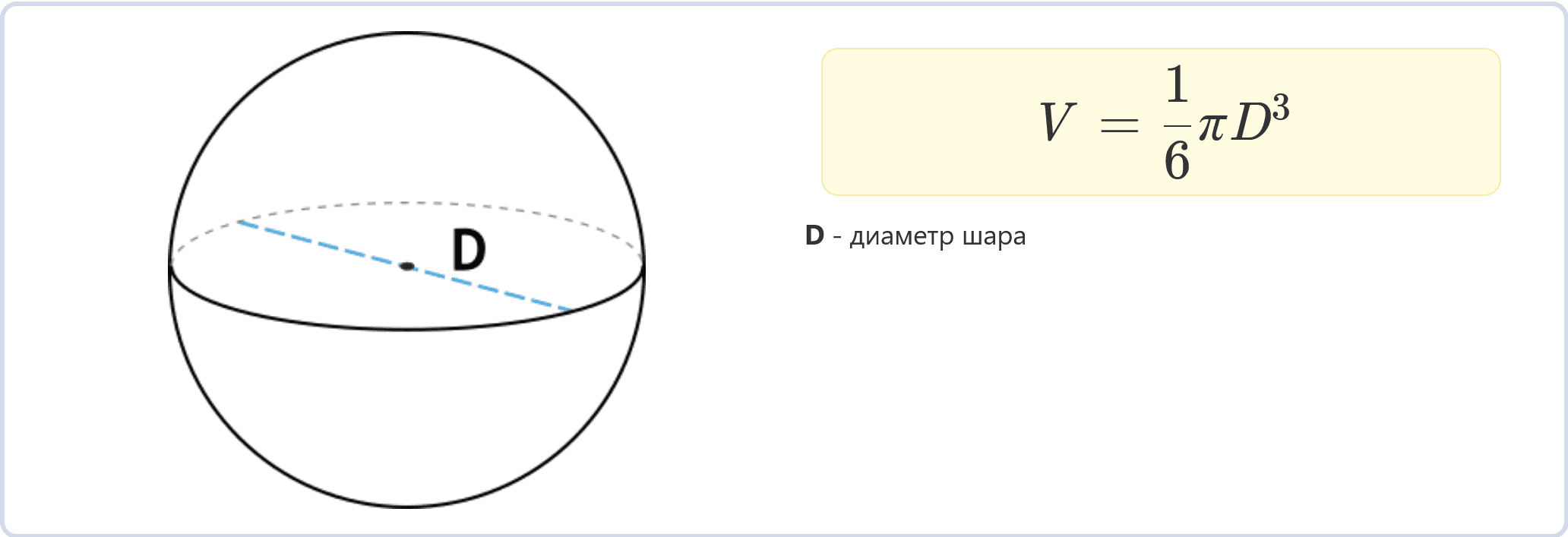
\(V = \dfrac{1}{6} \pi D^3\)
V – объем шара,
π (пи) – математическая константа,
D – диаметр шара.
Формула объема шара через длину окружности
Длина окружности шара – это расстояние вокруг его поверхности. Если известна длина окружности, то объем шара можно найти по формуле:
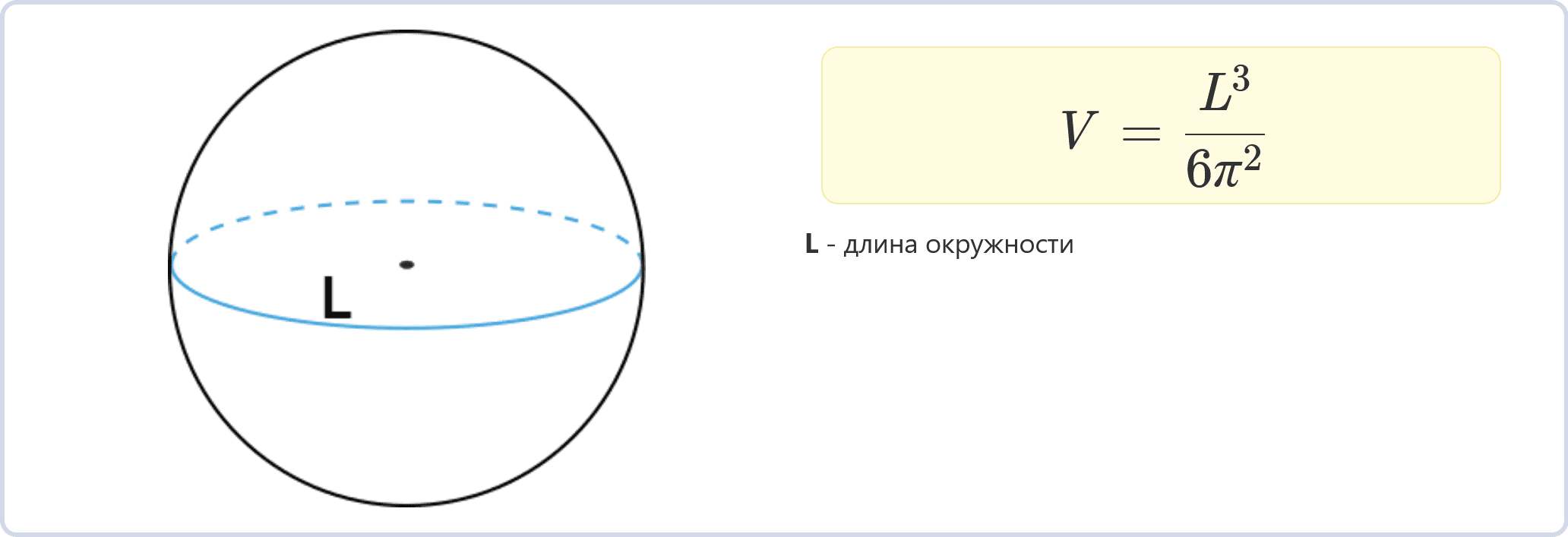
\(V = \dfrac{L^3}{6 \pi^2}\)
V – объем шара,
π (пи) – математическая константа,
L – длина окружности шара.
Формула объема шара через площадь поверхности
Площадь поверхности шара – это общая площадь его наружной поверхности. Если известна площадь поверхности, то объем шара можно вычислить так:
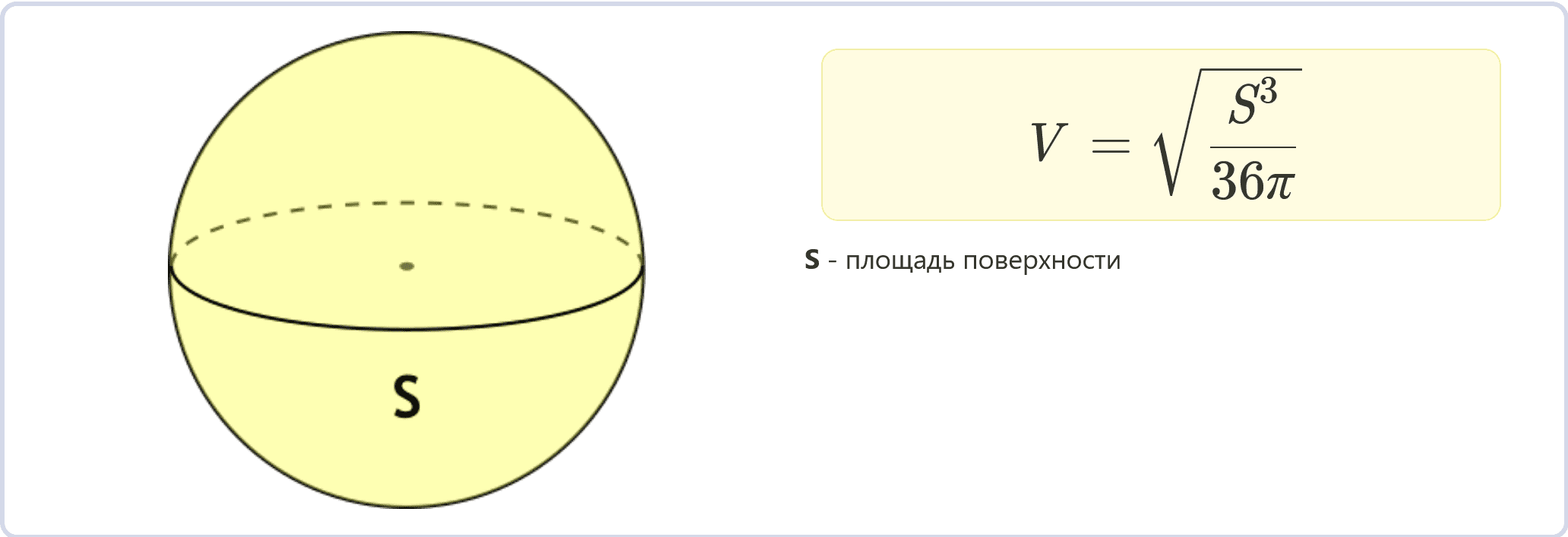
\(V = \sqrt{ \dfrac{S^3}{36 \pi}}\)
V – объем шара,
π (пи) – математическая константа,
S – площадь поверхности шара.
Калькулятор объема шара
Для более удобного и быстрого вычисления объема шара вы можете воспользоваться калькулятором. Введите известные данные (радиус, диаметр, длину окружности или площадь поверхности) и калькулятор автоматически рассчитает объем шара для вас.
Заключение
Знание формул для вычисления объема шара может быть полезным в различных областях, включая геометрию, физику и инженерию. Пользуясь правильными формулами и инструментами, вы сможете легко рассчитывать объем шаров и применять это знание в практических задачах.
Полезен ли материал?
12 / 1

