Объем параллелепипеда
Параллелепипед – это геометрическая фигура в трехмерном пространстве, которая обладает прямоугольной формой и имеет шесть граней. Его грани являются параллелограммами, и он имеет три пары параллельных сторон. Один из важных параметров, определяющих параллелепипед, это его объем, который показывает, сколько пространства он занимает. Рассмотрим, как можно вычислить объем параллелепипеда в разных случаях.
Прямоугольный параллелепипед
Прямоугольный параллелепипед обладает особыми свойствами, так как у него все углы прямые, а грани попарно перпендикулярны друг другу. В данном случае существует несколько способов вычисления объема.
Через три стороны
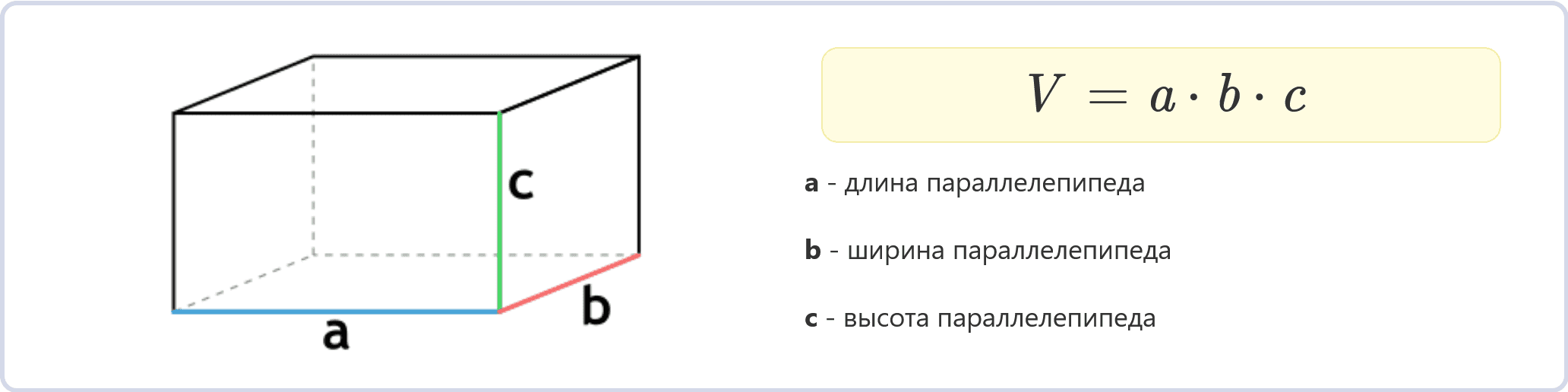
Формула объема прямоугольного параллелепипеда через длины его трех сторон (a, b и c) выглядит так:
V = a * b * c
Через площадь основания и высоту
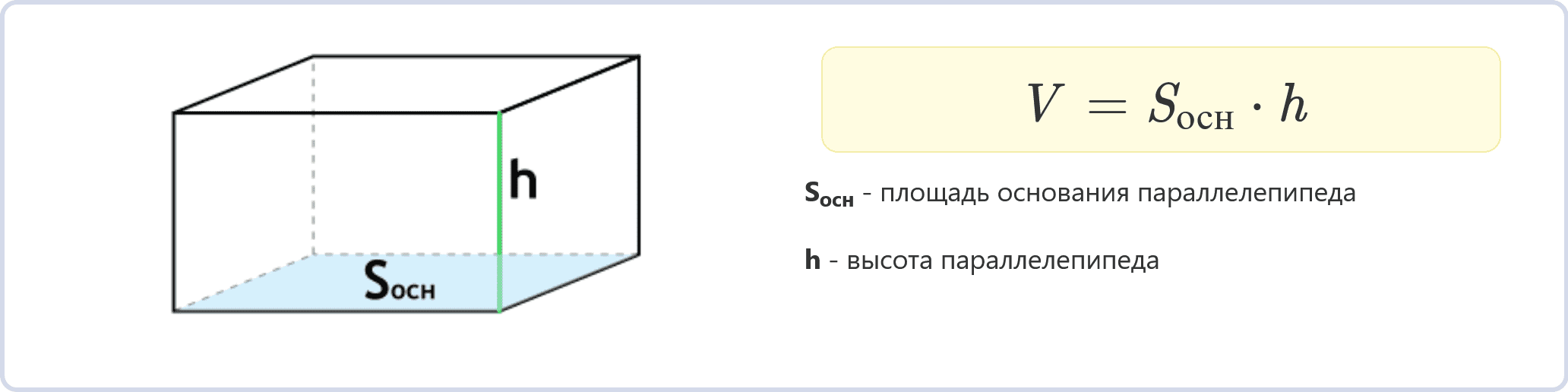
Если известна площадь одной из граней (Sосн) и высота (h), можно использовать следующую формулу:
V = Sосн * h
Наклонный параллелепипед
У наклонного параллелепипеда не все грани перпендикулярны друг другу, но он также может быть вычислен по разным параметрам.
Через длины сторон основания и высоту
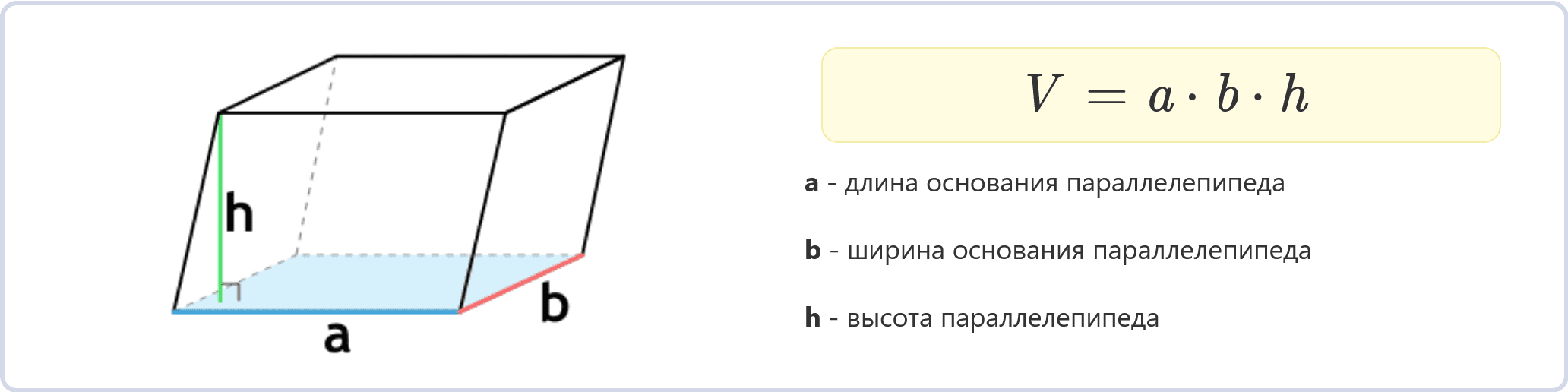
Если известны длина (a) и ширина (b) основания, а также высота (h), то формула объема будет следующей:
V = a * b * h
Через площадь основания и высоту
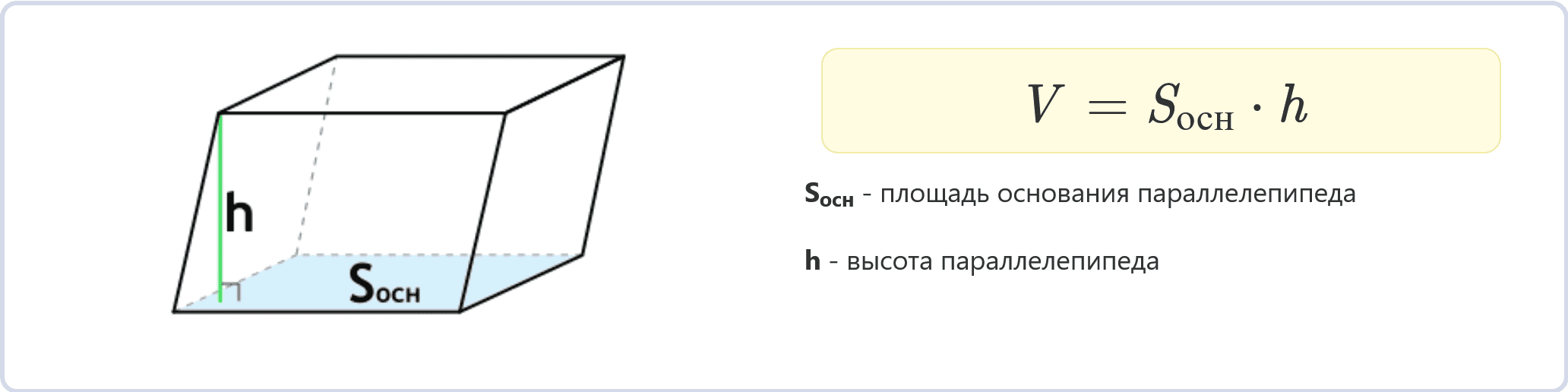
Аналогично, если известны площадь одной из граней (Sосн) и высота (h), можно использовать формулу:
V = Sосн * h
Вычисление объема параллелепипеда может быть полезным при проектировании, строительстве, а также в других областях, где важно определить объем занимаемого пространства.
Применение в реальной жизни
Понимание объема параллелепипеда имеет практическое значение во многих областях. В архитектуре и строительстве вычисление объема помогает определить необходимое количество материалов, например, для создания конструкций, упаковок или контейнеров. В инженерии это может быть полезным при разработке механизмов или устройств, где необходимо учесть объем и форму.
Таким образом, знание формул и методов вычисления объема параллелепипеда позволяет решать разнообразные задачи в различных областях и дает представление о том, как объем пространства связан с его параметрами.
Полезен ли материал?
2 / 8


