Объем куба
Куб – это одно из наиболее знакомых и простых трехмерных геометрических фигур. Он принадлежит к классу правильных многогранников и обладает рядом интересных свойств. Одним из ключевых параметров, характеризующих куб, является его объем. Объем куба представляет собой количество пространства, занимаемого данной фигурой. В этой статье мы рассмотрим понятие объема куба, его свойства и различные способы вычисления.
Определение объема куба
Объем куба – это мера трехмерного пространства, ограниченного шестью квадратными гранями. Все грани куба являются прямоугольниками одинаковой площади, а все его углы прямые. Куб является одним из регулярных полихедров, у которых все стороны и углы одинаковы. Он обладает рядом характерных свойств, таких как равенство всех ребер и граней.
Свойства куба
- Равные стороны и углы: Все стороны куба одинаковы по длине, и все углы прямые (равны 90 градусам).
- Симметрия: Куб обладает высокой степенью симметрии. Все его грани и ребра симметричны относительно центра куба.
- Равенство диагоналей: Диагонали параллельных граней куба равны друг другу и пересекаются в его центре.
- Объем и площадь: Объем куба тесно связан с его площадью поверхности. Площадь каждой грани куба равна квадрату длины его ребра. Объем можно выразить через длину ребра.
Способы вычисления объема куба
Объем куба можно вычислить различными способами, в зависимости от доступных данных. Вот некоторые из них:
Через ребро
Простейший способ – вычислить объем куба, возводя длину его ребра в куб. Формула:
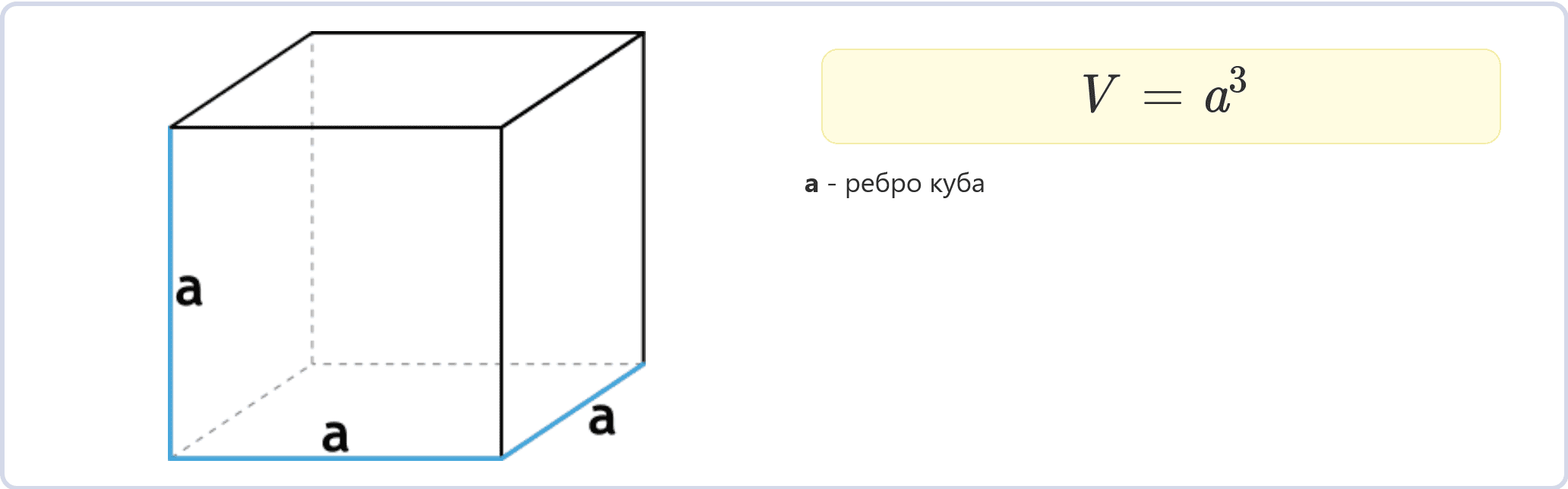
V = a3
где a – длина ребра.
Через диагональ грани
Если известна диагональ грани куба, можно использовать формулу:
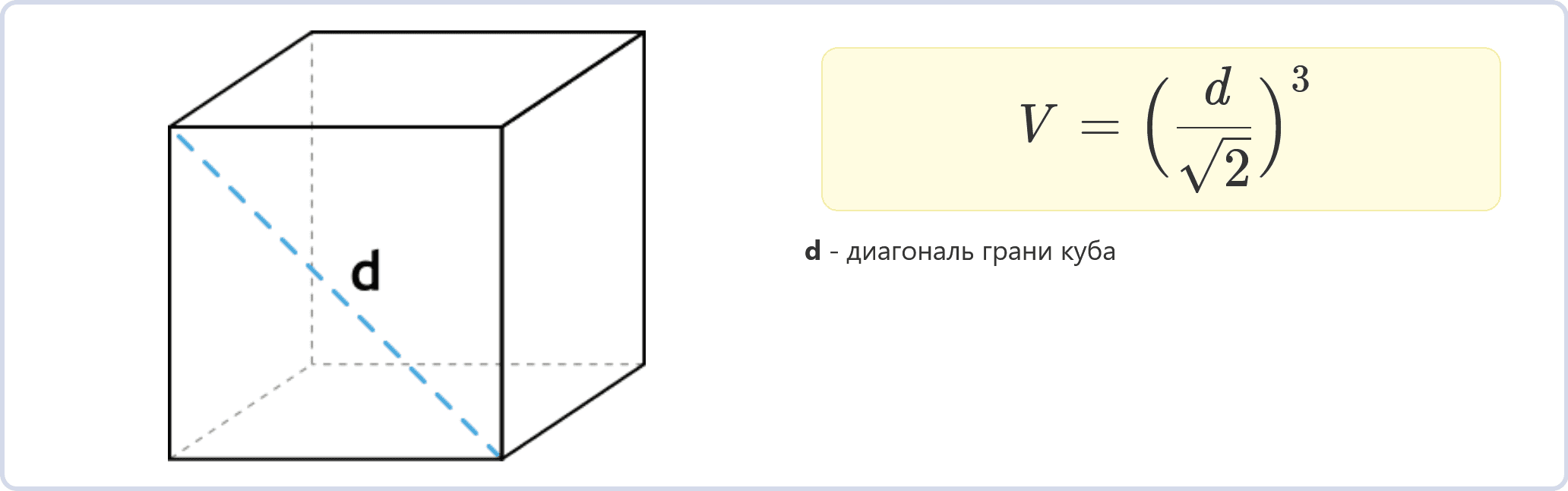
V = (d / √2)3
где d – диагональ грани.
Через периметр грани
При известном периметре грани куба можно воспользоваться формулой:
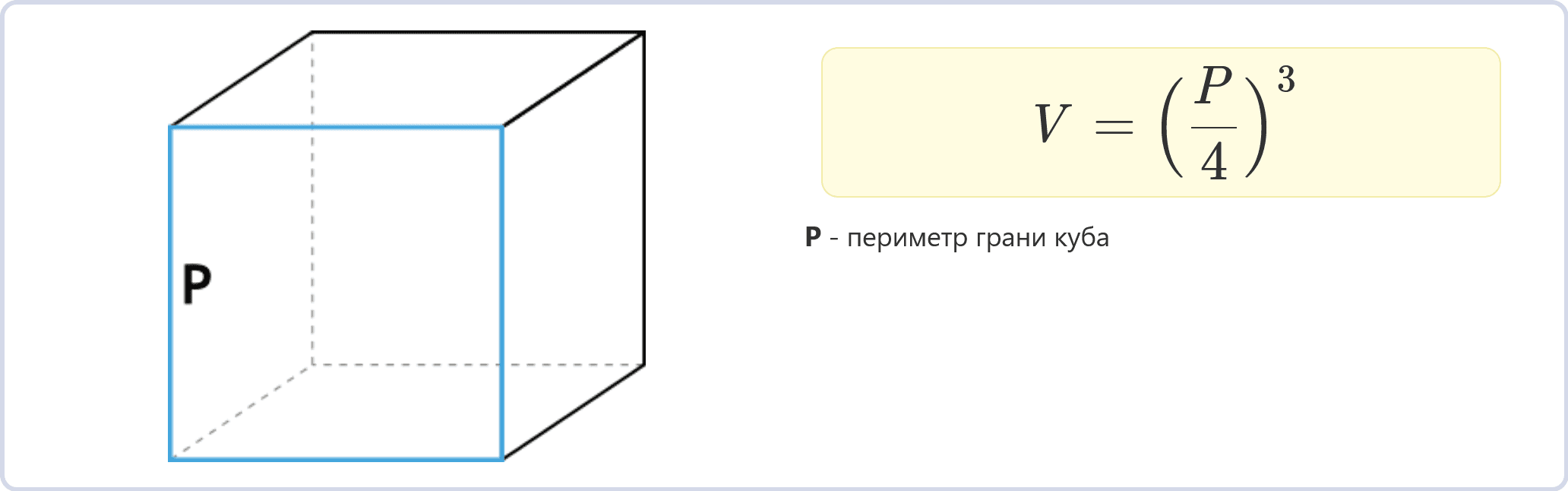
V = (P / 4)3
где P – периметр грани.
Через диагональ куба
Если дана диагональ куба, объем можно найти по формуле:
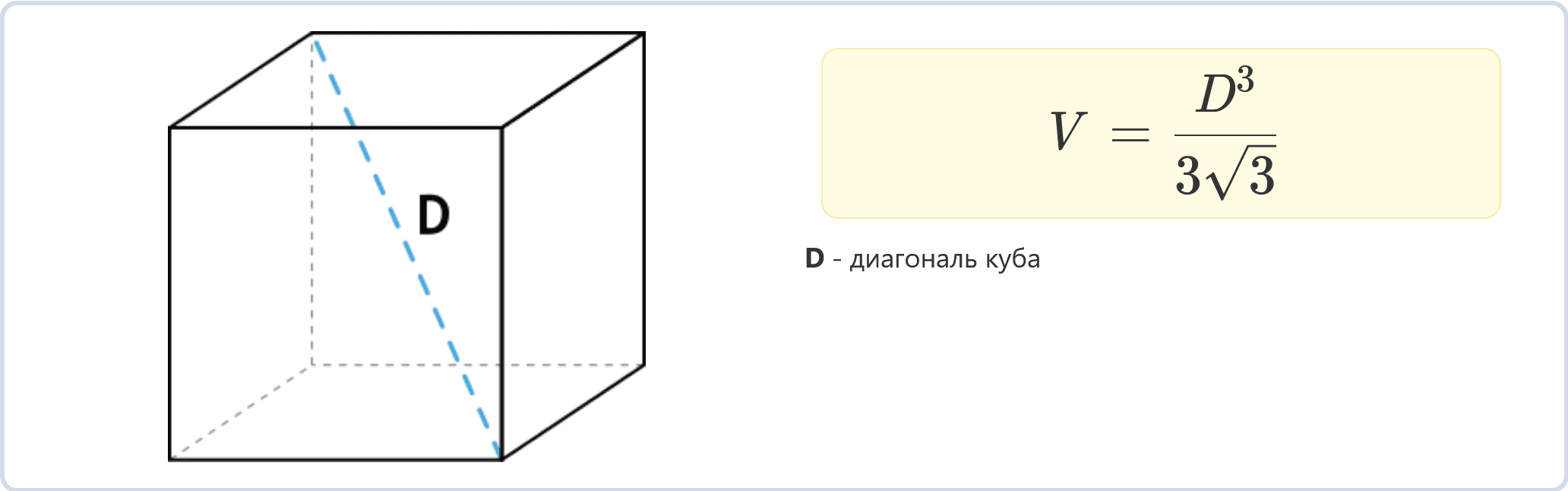
V = D3 / (3√3)
где D – диагональ куба.
Через площадь полной поверхности
Для вычисления объема через площадь полной поверхности используется формул:
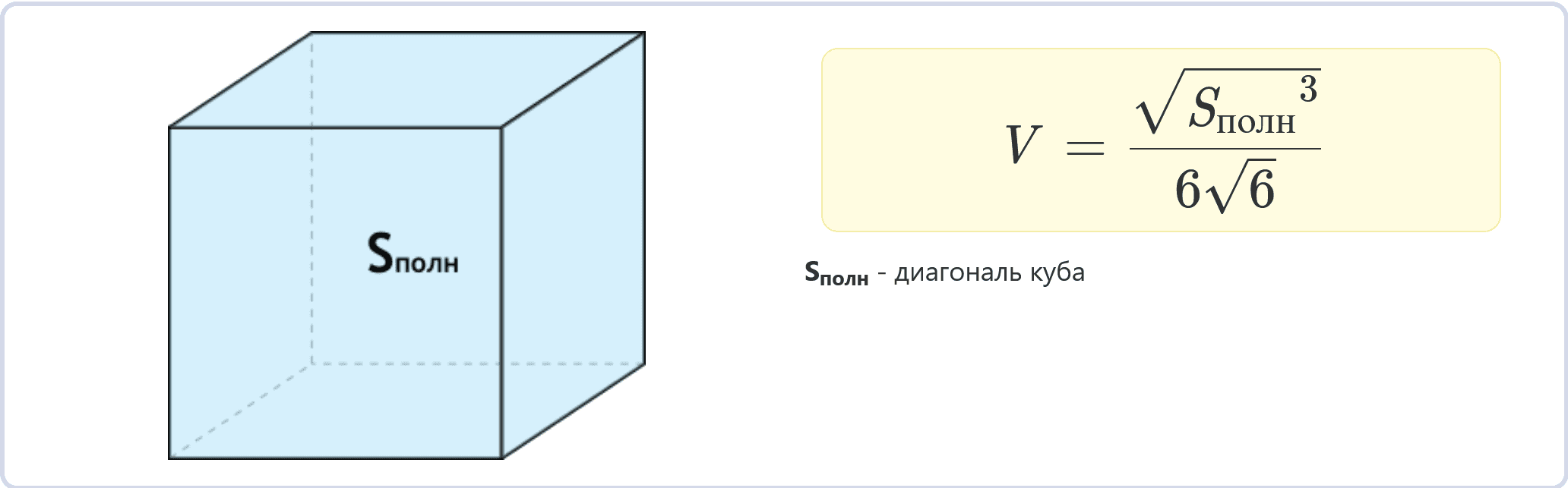
V = √(Sполн3) / 6√6
где Sполн – площадь полной поверхности.
Объем куба – это один из основных параметров, характеризующих этот геометрический объект. Зная длину ребра, диагональ грани или площадь полной поверхности, можно вычислить объем куба с использованием соответствующих формул. Этот параметр находит свое применение в различных областях, включая геометрию, физику и инженерное моделирование.
Полезен ли материал?
4 / 0


