Объем конуса
Конус – это одна из фигур, которая встречается в нашей повседневной жизни и имеет различные применения в науке, инженерии и других областях. В этой статье мы рассмотрим различные аспекты конуса, включая его определение, основные характеристики и методы вычисления объема. В частности, мы подробно изучим три основные формулы для вычисления объема конуса.
Определение конуса
Конус – это геометрическое тело, у которого есть одна кривая поверхность и одно основание, которое может быть круглым или любой другой формы. Вершина конуса соединяет кривую поверхность и основание. Высота конуса – это расстояние от вершины до основания, проведенное перпендикулярно к основанию. Конусы часто встречаются в природе и технике: от пирамидальных гор к шляпкам и транспортным средствам.
Формула объема прямого конуса
Для вычисления объема прямого конуса используется следующая формула:
Формула объёма конуса через радиус и высоту:
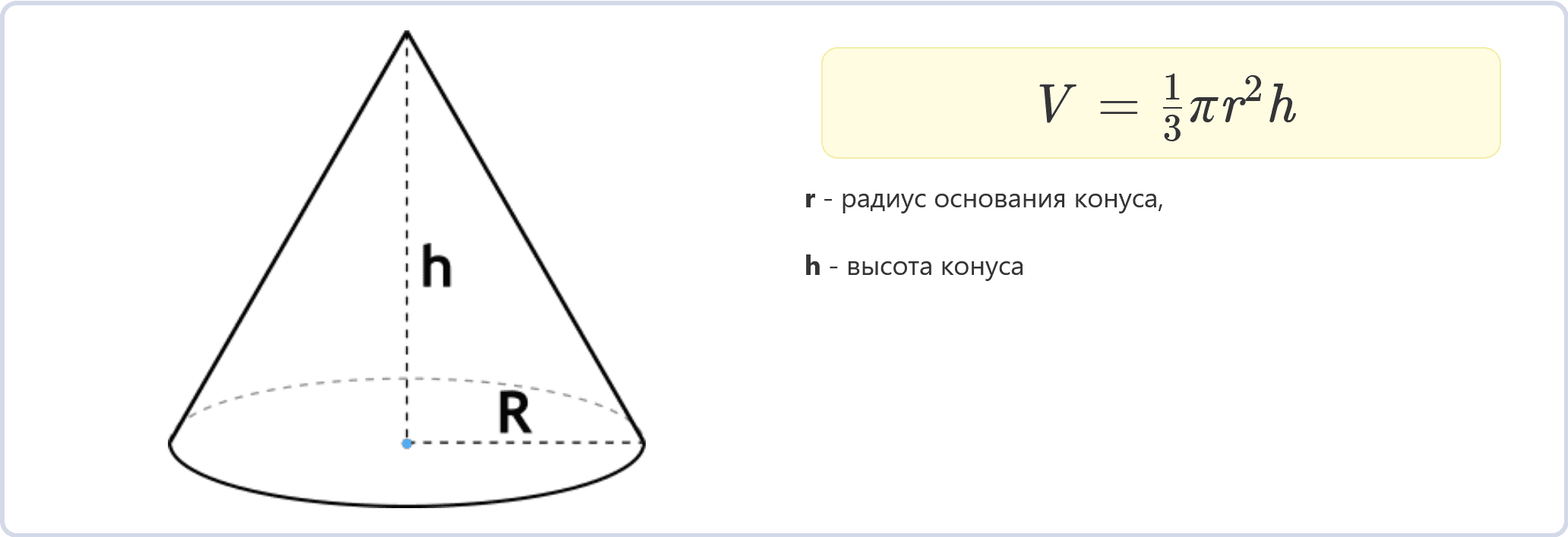
\[V = \frac{1}{3} \pi r^2 h\] Где:
- \(V\) – объем конуса,
- \(\pi\) (пи) – математическая константа, приближенно равная 3.14159,
- \(r\) – радиус основания конуса,
- \(h\) – высота конуса.
Чтобы рассчитать объем прямого конуса, вам понадобятся значения радиуса основания (\(r\)) и высоты (\(h\)). Просто подставьте их в формулу, выполните необходимые вычисления, и вы получите объем этого конуса.
Формула объема конуса через площадь основания
Есть еще один способ вычисления объема конуса, который зависит от площади его основания (\(S\)) и высоты (\(h\)):
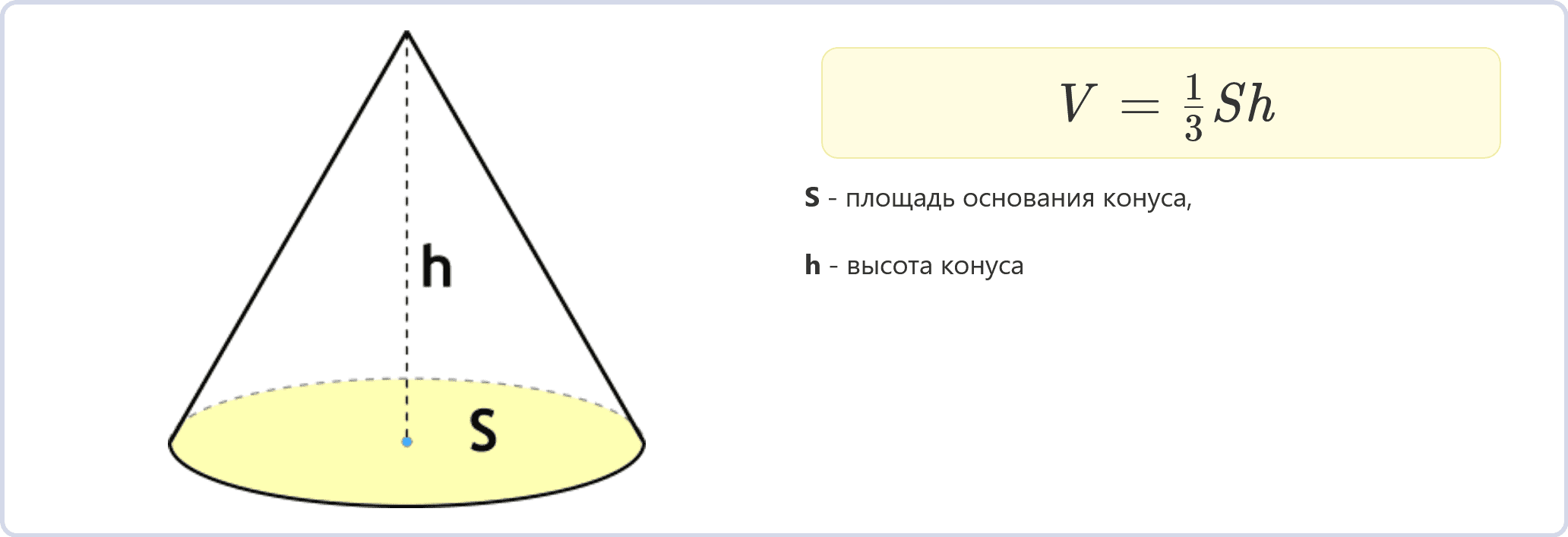
\[V = \frac{1}{3} S h\] Где:
- \(V\) – объем конуса,
- \(S\) – площадь основания конуса,
- \(h\) – высота конуса.
Эта формула удобна, если у вас есть информация о площади основания и высоте конуса.
Формула объема усеченного конуса
Усеченный конус имеет два основания – большее и меньшее. Для расчета его объема используется следующая формула:
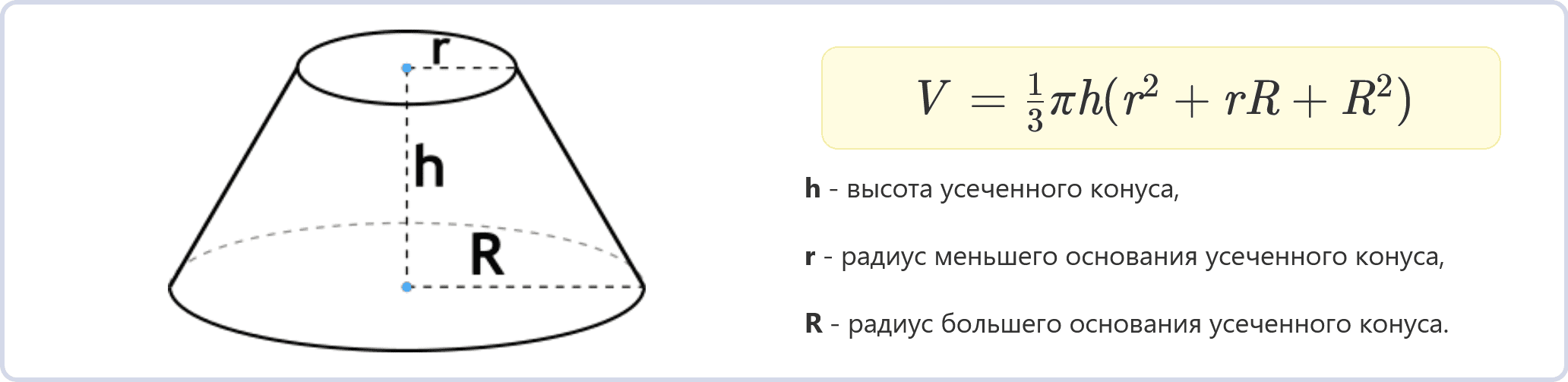
\[V = \frac{1}{3} \pi h(r^2 + r R + R^2)\] Где:
- \(V\) – объем усеченного конуса,
- \(\pi\) (пи) – математическая константа, приближенно равная 3.14159,
- \(h\) – высота усеченного конуса,
- \(r\) – радиус меньшего основания усеченного конуса,
- \(R\) – радиус большего основания усеченного конуса.
Чтобы рассчитать объем усеченного конуса, необходимо знать значения высоты (\(h\)), радиуса меньшего основания (\(r\)) и радиуса большего основания (\(R\)). Подставьте эти значения в формулу и выполните необходимые вычисления.
Знание этих формул полезно в различных областях, от геометрии до инженерии и строительства, и может пригодиться в решении практических задач.
Полезен ли материал?
16 / 2

