Вектором называется направленный отрезок AB; точка A – начало, точка B – конец вектора
Вектор обозначается либо двумя большими буквами – своим началом и концом: AB либо одной малой буквой: a.
Длину вектора a будем обозначать ∣a∣. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Определение длины вектора
- Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
- Длиной (модулем) вектора AB называется неотрицательное число, равное расстоянию между его началом и концом, то есть длина вектора – это длина отрезка AB. Длина AB обозначается |AB|
- Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Длина нулевого вектора 0 равна нулю. Длина единичного вектора e равна единице.
Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат.
Формула длины вектора для плоских задач
В случае плоской задачи модуль вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2
Формула длины вектора в трехмерном пространстве
В случае пространственной задачи модуль вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2 + az2
Примеры задач на вычисление длины вектора
Пример 1.
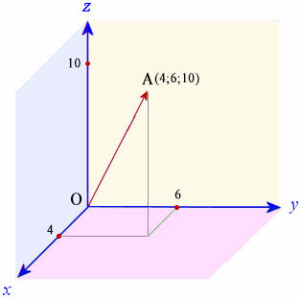Вектор
ОА имеет начальную точку в начале координат О (0; 0; 0) и конечную точку в А (4; 6; 10). Найдите длину вектора.
Решение:
|ОА| = √42+62+102
|ОА| = √152
|ОА| = 12,32
Пример 2.
Найти длину вектора a = {2; 4}.
Решение:
|a| = √22 + 42
|a| = √4 + 16
|a| = √20
|a| = 2√5
|a| = 4.47213595499958
Пример 3.
Найти длину вектора a = {-1; 0; -3}.
Решение:
|a| = √(-1)2 + 02 + (-3)2
|a| = √1 + 0 + 9
|a| = √10
Полезен ли материал?
3 / 1
