Квадрат — четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Одна из самых частых задач, связанных с квадратом — нахождение его площади. На этой странице мы подготовили 5 формул площади квадрата с возможностью рассчитать ее онлайн по любой из них с помощью удобного калькулятора.
Площадь квадрата: калькулятор и формулы
С помощью нашего бесплатного онлайн калькуляторы вы можете найти площадь квадрата следующими методами:
- По формуле площади квадрата через сторону
- По формуле площади квадрата через диагональ
- По формуле площади квадрата через радиус вписанной окружности
- По формуле площади квадрата через радиус описанной окружности
- По формуле площади квадрата через периметр
Формулы площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Формула площади квадрата через сторону
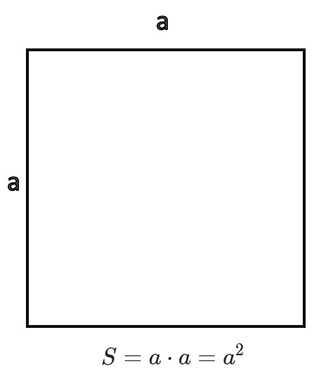
Если известна длина стороны, умножаем ее на то же число или возводим в квадрат.
S = a × a = a2, где S — площадь, a — сторона.
Формула площади квадрата через диагональ
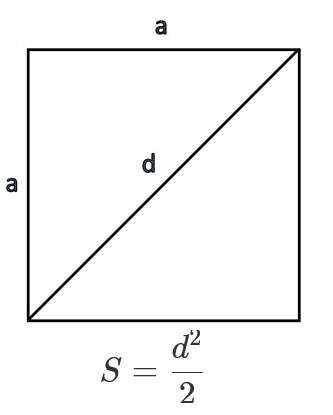
Если нам дана диагональ, возводим ее в квадрат и делим на два.
S = d2 : 2, где d — диагональ.
Формула площади квадрата через радиус вписанной окружности
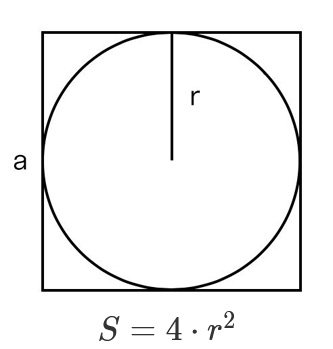
Если известен радиус вписанной окружности, умножаем его квадрат на четыре.
S = 4 × r2, где r — это радиус вписанной окружности.
Формула площади квадрата через радиус описанной окружности
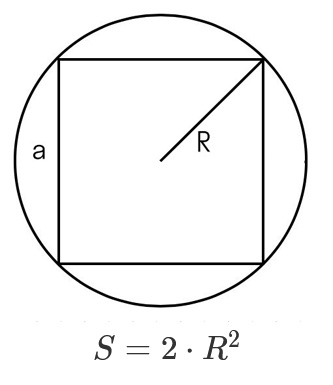
Если у нас есть радиус описанной окружности, возведем его в квадрат и умножим на два.
S = 2 × R2, где R — это радиус описанной окружности.
Формула площади квадрата через периметр
Если есть периметр, мы должны возвести его в квадрат и разделить на 16.
S = Р2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Будет ошибка, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Полезен ли материал?
2 / 3


