Площадь ромба и методы её вычисления

Ромб — это особый вид параллелограмма, у которого все стороны равны между собой, а углы между соседними сторонами равны. Площадь ромба — это важный параметр, который можно вычислить различными способами, в зависимости от доступной информации о фигуре. В данной статье рассмотрим ромб и каждый из трех методов вычисления его площади: через диагонали, через длину стороны и высоту, а также через полупериметр и длину стороны.

1. Ромб и его свойства

Ромб — это четырехугольник, у которого все стороны равны между собой (a₁ = a₂ = a₃ = a₄ = a) и углы между соседними сторонами равны (обычно обозначаются буквой “α”). Также в ромбе существуют следующие свойства:

• Диагонали ромба делят его на четыре равных равнобедренных треугольника.
• Противоположные углы ромба суммируются до 180°.
• Диагонали ромба перпендикулярны друг другу, и их точка пересечения является центром симметрии ромба.

2. Площадь ромба через диагонали

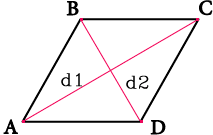
Для вычисления площади ромба через диагонали используется следующая формула:

S = (d1 * d2) / 2

где “d1” и “d2” — длины диагоналей ромба.

Этот метод подходит, когда известны длины обеих диагоналей ромба.

3. Площадь ромба через длину стороны и высоту

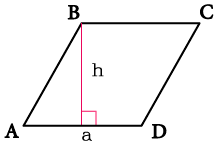
Если известны длина одной стороны ромба (a) и длина высоты, опущенной на эту сторону (h), то площадь ромба можно вычислить по формуле:

S = a * h

Этот метод подходит, когда известны длина одной стороны ромба и длина высоты, опущенной на эту сторону.

4. Площадь ромба через полупериметр и длину стороны

Если известна только длина одной стороны ромба (a), то можно воспользоваться формулой площади ромба через полупериметр (p) и длины стороны (a):

p = (a₁ + a₂ + a₃ + a₄) / 2

S = √(p * (p – a₁) * (p – a₂) * (p – a₃) * (p – a₄))

В ромбе все стороны равны, поэтому формулу можно упростить до:

p = 4 * a

S = √(p * (p – a) * (p – a) * (p – a) * (p – a))

S = √(a⁴)

Этот метод подходит, когда известна только длина одной стороны ромба.

5. Площадь ромба через сторону и угол

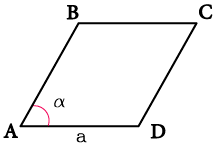
Площадь ромба можно вычислить ещё одним способом — через длину одной стороны и величину угла между этой стороной и одной из диагоналей. В данном случае, длина одной стороны ромба и величина угла могут быть известными. Для вычисления площади используется следующая формула:

S = a² * sin(α)

где:

• a — длина одной стороны ромба,
• α — величина угла между стороной a и одной из диагоналей.

Заключение

Таким образом, площадь ромба можно вычислить различными способами, в зависимости от того, какая информация о фигуре известна. Через диагонали, длину стороны и высоту, полупериметр и длину стороны, а также через длину стороны и величину угла — каждый метод позволяет найти площадь ромба в различных ситуациях. Зная эти формулы, можно легко определить площадь ромба и использовать этот параметр в решении различных геометрических задач.

Интересные факты о ромбе:

1. Симметрия: Ромб обладает несколькими осями симметрии. Центральная ось симметрии проходит через центр ромба и делит его на две симметричные части. Также ромб имеет оси симметрии, проходящие через середины каждой из его сторон.
2. Конструкция ромба: Ромб можно построить с помощью двух перпендикулярных диагоналей, проведенных из центра фигуры. Каждая диагональ делит ромб на два равных треугольника.
3. Ромбовидные узоры: Форма ромба часто используется в дизайне и создании ромбовидных узоров, которые могут быть найдены на тканях, плитках, стенах и других поверхностях.
4. Приложения в геометрии: Ромб применяется в геометрии и тригонометрии для решения различных задач, таких как нахождение площади фигуры, вычисление длин сторон, углов и диагоналей.

Формулы ромба:

1. Периметр ромба: P = 4a, где “a” – длина стороны ромба.
2. Площадь ромба через диагонали: S = (d1 * d2) / 2, где “d1” и “d2” – длины диагоналей ромба.
3. Площадь ромба через длину стороны и высоту: S = a * h, где “a” – длина стороны ромба, “h” – высота, опущенная на эту сторону.
4. Площадь ромба через полупериметр и длину стороны: S = a², где “a” – длина стороны ромба, “p” = 4a – полупериметр.
5. Площадь ромба через длину стороны и угол: S = a² * sin(θ), где “a” – длина стороны ромба, “θ” – угол между двумя сторонами.
6. Формула для нахождения длины диагоналей через длину стороны и угол: d1 = a / sin(θ), d2 = a / sin(π – θ), где “a” – длина стороны ромба, “θ” – угол между двумя сторонами.
7. Угол между диагоналями: θ = arccos((a² + a² – d²) / (2 * a * a)), где “a” – длина стороны ромба, “d” – длина одной из диагоналей.

Эти формулы позволяют решать различные задачи, связанные с ромбами, и использовать их свойства в различных областях математики и практических приложениях.

 

Полезен ли материал?

ДаНет

7 / 2

#Калькуляторы #Математика #Площадь