Площадь равнобедренной трапеции, в которую можно вписать окружность
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
1. Площадь через высоту (диаметр вписанной окружности) и угол при основании

S = (h2)/(sin(α))
где h – высота равнобедренной трапеции, α – угол при основании равнобедренной трапеции.
2. Площадь через основания и угол при основании

S = (a * b)/(sin(α))
где a и b – основания равнобедренной трапеции, α – угол при основании равнобедренной трапеции.
3. Площадь через основания и радиус вписанной окружности

S = r(a + b)
r = (sqrt(a * b))/2
где a и b – основания равнобедренной трапеции, r – радиус вписанной окружности.
4. Площадь через основания

S = sqrt(a * b) * (a + b)/2
где a и b – основания равнобедренной трапеции.
5. Площадь через основания и боковую сторону
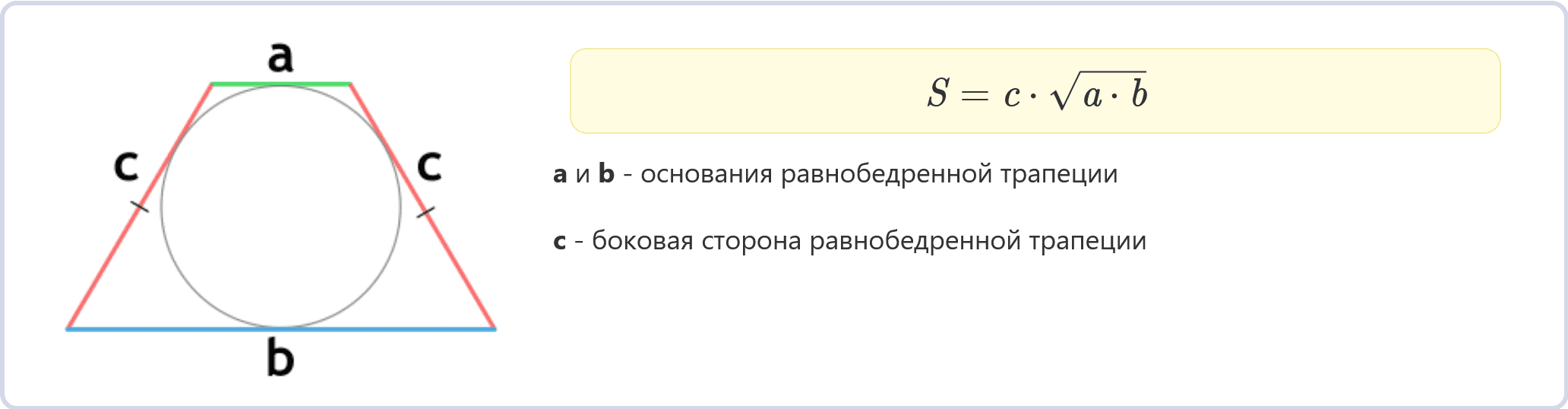
S = c * sqrt(a * b)
где a и b – основания равнобедренной трапеции, c – боковая сторона равнобедренной трапеции.
6. Площадь через основания и среднюю линию

S = m * sqrt(a * b)
где a и b – основания равнобедренной трапеции, m – средняя линия равнобедренной трапеции.
Полезен ли материал?
1 / 0


